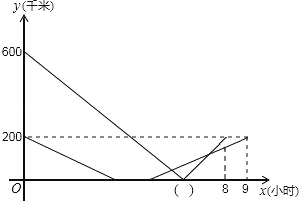
【题目】甲、乙两车在连通A、B、C三地的公路上行驶,甲车从A地出发匀速向C地行驶,同时乙车从C地出发匀速向b地行驶,到达B地并在B地停留1小时后,按原路原速返回到C地.在两车行驶的过程中,甲、乙两车距B地的路程y(千米)与行驶时间x(小时)之间的函数图象如图所示,请结合图象回答下列问题:
(1)求甲、乙两车的速度,并在图中( )内填上正确的数:
(2)求乙车从B地返回到C地的过程中,y与x之间的函数关系式;
(3)当甲、乙两车行驶到距B地的路程相等时,甲、乙两车距B地的路程是多少?
参考答案:
【答案】(1)6;(2)y=50x-250(5≤x≤9).(3)![]() 或100千米.
或100千米.
【解析】
试题分析:(1)由已知图象求出甲、乙的速度.
(2)根据图象上的点先求出乙车从B地返回到C地的函数解析式,
(3)再由设甲车从A地到B地的函数解析式是y1=k1x+b1,和甲车从B地到C地的函数解析式是y2=k2x+b2,由已知求出解析式结合(2)求出的解析式求解.
试题解析:(1)由已知图象得:甲的速度为:(600+200)÷8=100km/h,乙的速度为(200+200)÷(9-1)=50km/h,
∵甲的速度为:100km/h,与B地相距600km,
∴时间=![]() =6,
=6,
(2)设乙车从B地返回到C地的函数解析式是y=kx+b,
∵乙的速度为(200+200)÷(9-1)=50km/h,
∴乙到B地的时间是200÷50=4(小时),
4+1=5,
即点M(5,0),如图,
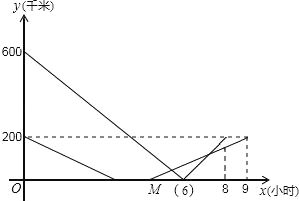
∵图象经过M(5,0),(9,200)两点.
∴5k+b=0,9k+b=200
解得:![]() ,
,
∴y=50x-250,
答:乙车从B地返回到C地的过程中,y与x之间的函数关系式为y=50x-250(5≤x≤9).
(3)设甲车从A地到B地的函数解析式是y1=k1x+b1,
∵图象经过(0,600),(6,0)两点,
∴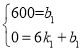 ,解得:
,解得: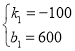 ,
,
∴y1=-100x+600,
设甲车从B地到C地的函数解析式是y2=k2x+b2,
∵图象经过(8,200),(6,0)两点,
∴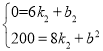 ,解得:
,解得: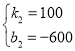 ,
,
∴y2=100x-600,
由 和
和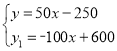 ,
,
解得:y=![]() (千米)或y=100(千米).
(千米)或y=100(千米).
答:当甲、乙两车行驶到距B地的路程相等时,甲、乙两车距B地的路程是![]() 或100千米.
或100千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在﹣3,﹣2,2,1四个实数中,最大的实数是( )
A. ﹣3 B. ﹣2 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点M(m,1)在一次函数y=x﹣2的图象上,则m=__.
-
科目: 来源: 题型:
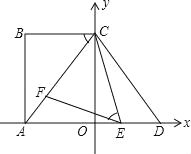
查看答案和解析>>【题目】如图:在平面直角坐标系中,点A、C分别在x轴负半轴、y轴正半轴上,且四边形ABCD为矩形,AB=4,点D与点A关于原点O成中心对称,tan∠ACB=
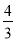 ,点E、F分别是线段AD、AC上的动点(点E不与点A、D重合),且∠CEF=∠ACB.
,点E、F分别是线段AD、AC上的动点(点E不与点A、D重合),且∠CEF=∠ACB.(1)求AC的长和点D的坐标;
(2)说明△AEF与△DCE相似;
(3)点M在第二象限,且在直线BC的下方,点N在平面内,是否存在这样点M,使得以点B、C、M、N为顶点的四边形是矩形,且矩形的长:宽=4:3?若存在,请直接写出点M的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:x2﹣4y2=__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,BD垂直平分AC,垂足为点F,E为四边形ABCD外一点,且∠ADE=∠BAD,AE⊥AC.
(1)求证:四边形ABDE是平行四边形;
(2)如果DA平分∠BDE,AB=5,AD=6,求AC的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】AD,AE分别是等边三角形ABC的高和中线,则AD 与AE 的大小关系为____.
相关试题

