【题目】市园林处为了对一段公路进行绿化,计划购买![]() ,
,![]() 两种风景树共900棵.
两种风景树共900棵.![]() ,
,![]() 两种树的相关信息如下表:
两种树的相关信息如下表:
品种 项目 | 单价(元 | 成活率 |
| 80 |
|
| 100 |
|
若购买![]() 种树
种树![]() 棵,购树所需的总费用为
棵,购树所需的总费用为![]() 元.
元.
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)若购树的总费用不超过82 000元,则购![]() 种树不少于多少棵?
种树不少于多少棵?
(3)若希望这批树的成活率不低于![]() ,且使购树的总费用最低,应选购
,且使购树的总费用最低,应选购![]() ,
,![]() 两种树各多少棵?此时最低费用为多少?
两种树各多少棵?此时最低费用为多少?
参考答案:
【答案】(1)y![]() 且为整数);(2)购
且为整数);(2)购![]() 种树为:
种树为:![]() 且为整数.(3)应购
且为整数.(3)应购![]() 种树600棵,
种树600棵,![]() 种树300棵.
种树300棵.
【解析】
(1)根据购树的总费用![]() 买
买![]() 种树的费用
种树的费用![]() 买
买![]() 种树的费用,化简后便可得出
种树的费用,化简后便可得出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)根据(1)得到的关系式,然后将所求的条件代入其中,然后判断出购买![]() 种树的数量;
种树的数量;
(3)先用![]() 种树的成活的数量
种树的成活的数量![]() 种树的成活的数量
种树的成活的数量![]() 树的总量
树的总量![]() 平均成活率来判断出
平均成活率来判断出![]() 的取值,然后根据函数的性质判断出最佳的方案.
的取值,然后根据函数的性质判断出最佳的方案.
解:(1)![]()
![]() 且为整数);
且为整数);
(2)由题意得:![]() ,
,
解得:![]() ,
,
又因为计划购买![]() ,
,![]() 两种风景树共900棵,
两种风景树共900棵,
所以![]() ,
,
即购![]() 种树为:
种树为:![]() 且为整数.
且为整数.
(3)![]()
![]()
![]()
![]()
![]() 随
随![]() 的增大而减小.
的增大而减小.
![]() 当
当![]() 时,购树费用最低为
时,购树费用最低为![]() (元
(元![]() .
.
当![]() 时,
时,![]() ,
,
![]() 此时应购
此时应购![]() 种树600棵,
种树600棵,![]() 种树300棵.
种树300棵.
-
科目: 来源: 题型:
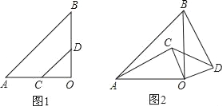
查看答案和解析>>【题目】如图1、图2,△AOB,△COD均是等腰直角三角形,∠AOB=∠COD=90°,
(1)在图1中,AC与BD相等吗?请说明理由;
(2)若△COD绕点O顺时针旋转一定角度后,到达图2的位置,请问AC与BD还相等吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市从
 年
年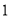 月
月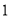 日开始实施阶梯电价制,居民生活用电价格方案如下:
日开始实施阶梯电价制,居民生活用电价格方案如下:档次
月用电量
电价
(单位:元
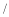 度)
度)春秋季(
 ,
,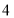 ,
,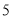 ,
,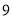 ,
,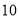 ,
,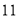 月)
月)冬夏季(
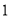 ,
,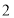 ,
,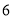 ,
,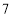 ,
,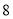 ,
,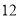 月)
月)第
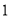 档
档不超过
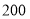 度的部分
度的部分不超过
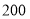 度的部分
度的部分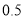
第
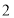 档
档超过
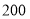 度但不超过
度但不超过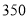 度的部分
度的部分超过
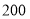 度但不超过
度但不超过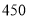 度的部分
度的部分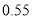
第
 档
档超过
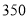 度的部分
度的部分超过
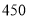 度的部分
度的部分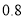
例:若某用户
 年
年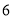 月的用电量为
月的用电量为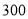 度,则需交电费为:
度,则需交电费为: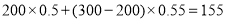 (元).
(元).(1)若小辰家
 年
年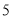 月的用电量为
月的用电量为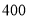 度,则需交电费多少元?
度,则需交电费多少元?(2)若小辰家
 年
年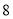 月和
月和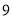 月用电量相同,共交电费
月用电量相同,共交电费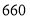 元,问小辰家
元,问小辰家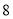 月份用多少度电?
月份用多少度电? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
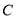 在线段
在线段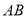 上,
上,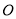 是线段
是线段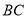 的中点.
的中点.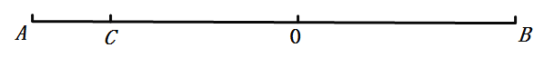
(1)在线段
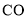 上,求作点
上,求作点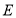 ,使
,使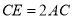 .
.(要求:尺规作图,不写作法保留作图痕迹)
(2)在(1)的条件下,
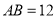 ,
,①若
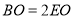 ,求
,求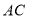 的长;
的长;②若点
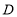 在线段
在线段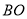 上,且
上,且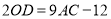 ,请你判断点
,请你判断点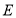 是哪条线段的中点,并说明理由.
是哪条线段的中点,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】(题文)1978年,以中共十一届三中全会为标志,中国开启了改革开放历史征程.40年众志成城,40年砥砺奋进,40年春风化雨,中国人民用双手书写了国家和民族发展的壮丽史诗.下图是1994—2017年三次产业对GDP的贡献率统计图(三次产业是指:第一产业是指农、林、牧、渔业(不含农、林、牧、渔服务业);第二产业是指采矿业(不含开采辅助活动),制造业(不含金属制品、机械和设备修理业),电力、热力、燃气及水生产和供应业,建筑业;第三产业即服务业,是指除第一产业、第二产业以外的其他行业).下列推断不合理的是( )
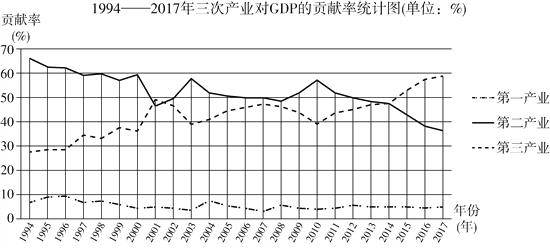
A. 2014年,第二、三产业对GDP的贡献率几乎持平;
B. 改革开放以来,整体而言三次产业对GDP的贡献率都经历了先上升后下降的过程;
C. 第三产业对GDP的贡献率增长速度最快的一年是2001年;
D. 2006年,第二产业对GDP的贡献率大约是第一产业对GDP的贡献率的10倍.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
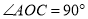 ,
,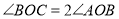 ,射线
,射线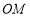 绕点
绕点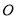 从射线
从射线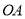 位置开始按顺时针方向以每秒
位置开始按顺时针方向以每秒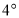 的速度旋转,到
的速度旋转,到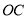 停止;同时射线
停止;同时射线 绕点
绕点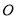 从射线
从射线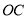 位置开始按逆时针方向以每秒
位置开始按逆时针方向以每秒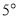 的速度旋转.
的速度旋转.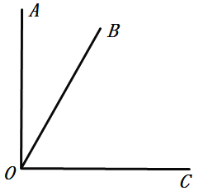
设当旋转时间为
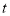 秒时,
秒时,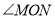 为
为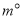 (
(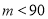 ).
).(1)填空:当
 秒,求
秒,求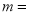 _____________;
_____________;(2)若
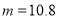 ,且
,且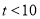 时,求
时,求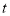 的值;
的值;(3)若射线
 旋转到
旋转到 后立即返回,按顺时针方向旋转,到
后立即返回,按顺时针方向旋转,到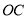 停止.用含
停止.用含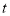 的式子表示
的式子表示 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用火柴棍分别拼成一排三角形组成的图形和一排正方形组成的图形,如果搭建三角形和正方形一共用了2020根火柴,且三角形的个数比正方形的个数多4个,则搭建三角形的个数是( )

A.402 B.406 C.410 D.420
相关试题

