【题目】如图,M是平行四边形ABCD的AB边中点,CM交BD于点E,则图中阴影部分的面积与平行四边形ABCD的面积的比是( )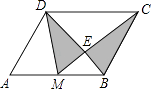
A.1:3
B.1:4
C.1:6
D.5:12
参考答案:
【答案】A
【解析】如右图,过E作GH⊥CD,分别交AB、CD于H、G,
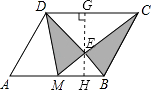
设EH=h,BM=a,S△BEM= ![]() ah=x,那么
ah=x,那么
∵M是AB中点,
∴BM= ![]() AB,
AB,
∵四边形ABCD是,
∴AB=CD,AB∥CD,
∴AB=CD=2a,
∵AB∥CD,
∴△BME∽△DCE,
∴EH:GE=BM:CD=1:2,
∴GH=3h,
∴S四边形ABCD=AB×GH=2a×3h=6ah=12x,
S△CBE=S△MBC﹣S△BME= ![]() a3h﹣
a3h﹣ ![]() ah=ah=2x,
ah=ah=2x,
同理有S△MED=2x,
S阴影=S△CBE+S△MED=4x,
∴S阴影:S四边形ABCD=4x:12x=1:3.
所以答案是:A.
【考点精析】通过灵活运用平行四边形的性质和相似三角形的判定与性质,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在A市正北300km处有B市,(1)以A市为原点,东西方向的直线为x轴,南北方向的直线为y轴,并以100km为1个单位建立平面直角坐标系.
(2)根据气象台预报,今年7号台风中心位置现在C(5,2)处,并以60千米/时的速度自东向西移动,台风影响范围半径为200km,问经几小时后,B市将受到台风影响?并画出示意图.
-
科目: 来源: 题型:
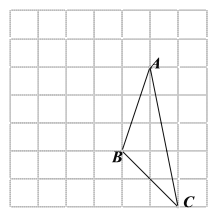
查看答案和解析>>【题目】画图(只能借助于网格)并填空:
如图,每个小正方形的边长为
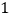 个单位,每个小正方形的顶点叫格点.
个单位,每个小正方形的顶点叫格点.(1)将
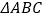 向左平移
向左平移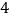 格,再向上平移
格,再向上平移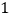 格,请在图中画出平移后的
格,请在图中画出平移后的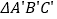 ;
;(2)
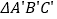 的面积为 ;
的面积为 ;(3)利用网格在图中画出△ABC的中线
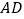 ,高线
,高线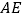 ;
;(4)在图中能使
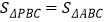 的格点
的格点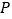 的个数有 个(点
的个数有 个(点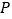 异于
异于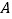 ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】把不等式组
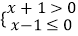 的解集表示在数轴上,正确的是( )
的解集表示在数轴上,正确的是( )
A.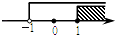
B.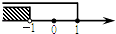
C.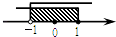
D.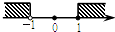
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)用不同的方法计算如图中阴影部分的面积得到的等式: ;
(2)如图是两个边长分别为
 、
、 、
、 的直角三角形和一个两条直角边都是
的直角三角形和一个两条直角边都是 的直角三角形拼成,试用不同的方法计算这个图形的面积,你能发现什么?说明理由;
的直角三角形拼成,试用不同的方法计算这个图形的面积,你能发现什么?说明理由;(3)根据上面两个结论,解决下面问题:若如图中,直角
 三边a、
三边a、 、c,
、c,①满足
 ,ab=18,求
,ab=18,求 的值;
的值;②在①的条件下,若点
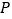 是边
是边 上的动点,连接
上的动点,连接 ,求线段
,求线段 的最小值;
的最小值;③若
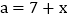 ,
, ,且
,且 ,则
,则 的值是 .
的值是 . 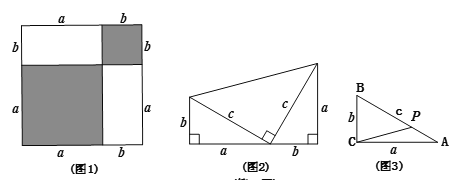
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学校组织的游艺会上,投飞标游艺区游戏区规则如下,如图投到A区和B区的得分不同,A区为小圆内部分,B区为大圆内小圆外部分(掷中一次记一个点)现统计小华、小明和小芳掷中与得分情况如图所示.

(1)求掷中A区、B区一次各得多少分?
(2)依此方法计算小明的得分为多少分?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(探究发现)
如图1,在△ABC中,点P是内角∠ABC和外角∠ACD的角平分线的交点,试猜想∠P与∠A之间的数量关系,并证明你的猜想.

(迁移拓展)
如图2,在△ABC中,点P是内角∠ABC和外角∠ACD的n等分线的交点,即∠PBC=
 ∠ABC,∠PCD=
∠ABC,∠PCD= ∠ACD,
∠ACD,试猜想∠P与∠A之间的数量关系,并证明你的猜想.
(应用创新)
已知,如图3,AD、BE相交于点C,∠ABC、∠CDE、∠ACE的角平分线交于点P,∠A=35°,∠E=25°,则∠BPD= .
相关试题

