【题目】(6分)在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,表是活动进行中的一组统计数据:
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数m | 68 | 109 | 136 | 345 | 368 | 701 |
摸到乒乓球的频率 | 0.68 | 0.73 | 0.68 | 0.69 | 0.70 | 0.70 |
(1)请估计:当n很大时,摸到白球的频率将会接近________;
(2)假如你去摸一次,你摸到白球的概率是_______,摸到黑球的概率是_______;
(3)试估算口袋中黑、白两种颜色的球各有多少只?
参考答案:
【答案】(1)![]() ;(2)白球概率
;(2)白球概率![]() ;黑球概率
;黑球概率![]() ;(3)白球数
;(3)白球数![]() ;黑球数
;黑球数![]() .
.
【解析】
试题当试验次数很大时,实验频率趋于理论概率.白球概率等于白球数除以总球数.
试题解析:(1)当试验次数很大时,实验频率趋于理论概率.所以当![]() 很大时,由表格知道摸到白球的频率为
很大时,由表格知道摸到白球的频率为![]() .(2)白球概率
.(2)白球概率![]() ;黑球概率为
;黑球概率为![]() ;(3)白球数等于总球数乘以白球概率
;(3)白球数等于总球数乘以白球概率![]() ;黑球数
;黑球数![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】同时抛掷A,B两个均匀的小立方体(每个面上分别标有数字1,2,3,4,5,6),设两立方体朝上的数字分别为x,y,并以此确定点P(x,y),那么点P落在直线y=-2x+9上的概率为( )
A.
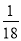 B.
B. 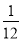 C.
C. 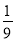 D.
D. 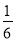
-
科目: 来源: 题型:
查看答案和解析>>【题目】四张扑克牌的牌面如图1,将扑克牌洗匀后,如图2背面朝上放置在桌面上,小明和小亮设计了A、B两种游戏方案:
方案A:随机抽一张扑克牌,牌面数字为5时小明获胜;否则小亮获胜.
方案B:随机同时抽取两张扑克牌,两张牌面数字之和为偶数时,小明获胜;否则小亮获胜.
请你帮小亮选择其中一种方案,使他获胜的可能性较大,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在街头巷尾会遇到一类“摸球游戏”,摊主的游戏道具是把分别标有数字1,2,3的3个白球和标有数字4,5,6的3个黑球(球除颜色外,其他均相同)放在口袋里,让你摸球,规定:每付3元钱就玩一局,每局连续摸两次,每次只能摸一个,第一次摸完后把球放回口袋里搅匀后再摸一次,若前后两次摸得的都是白球,摊主就送你10元钱的奖品.
(1)用列表法列举出摸出的两球可能出现的结果;
(2)求出获奖的概率;
(3)如果有50个人每人各玩一局,摊主会从这些人身上骗走多少钱?请就这一结果写一句劝诫人们不要参与摸球游戏的忠告语.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 箱中装有3张相同的卡片,它们分别写有数字1,2,4;
箱中装有3张相同的卡片,它们分别写有数字1,2,4; 箱中也装有3张相同的卡片,它们分别写有数字2,4,5;现从
箱中也装有3张相同的卡片,它们分别写有数字2,4,5;现从 箱、
箱、 箱中各随机地取出1张卡片,请你用画树形(状)图或列表的方法求:
箱中各随机地取出1张卡片,请你用画树形(状)图或列表的方法求:(1)两张卡片上的数字恰好相同的概率.
(2)如果取出
 箱中卡片上的数字作为十位上的数字,取出
箱中卡片上的数字作为十位上的数字,取出 箱中卡片上的数字作为个位上的数字,求两张卡片组成的两位数能被3整除的概率.
箱中卡片上的数字作为个位上的数字,求两张卡片组成的两位数能被3整除的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.

(1)求证:△ADC≌△CEB.
(2)AD=5cm,DE=3cm,求BE的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有一项资助贫困生的公益活动由你来主持,每位参与者需交赞助费5元,活动规则如下:如图是两个可以自由转动的转盘,每个转盘被分成6个相等的扇形,参与者转动这两个转盘,转盘停止后,指针各自指向一个数字,(若指针在分格线上,则重转一次,直到指针指向某一数字为止),若指针最后所指的数字之和为12,则获得一等奖,奖金20元;数字之和为9,则获得二等奖,奖金10元;数字之和为7,则获得三等奖,奖金为5元;其余均不得奖;此次活动所集到的赞助费除支付获奖人员的奖金外,其余全部用于资助贫困生的学习和生活;
(1)分别求出此次活动中获得一等奖、二等奖、三等奖的概率;
(2)若此次活动有2000人参加,活动结束后至少有多少赞助费用于资助贫困生?

相关试题

