Question

【题目】数学兴趣活动课上，小明将等腰△ABC的底边BC与直线1重合，问：

（1）已知AB＝AC＝6，∠BAC＝120°，点P在BC边所在的直线l上移动，根据“直线外一点到直线上所有点的连线中垂线段最短”，小明发现AP的最小值是　 　；

（2）为进一步运用该结论，小明发现当AP最短时，在Rt△ABP中，∠P＝90°，作了AD平分∠BAP，交BP于点D，点E、F分别是AD、AP边上的动点，连接PE、EF，小明尝试探索PE+EF的最小值，为转化EF，小明在AB上截取AN，使得AN＝AF，连接NE，易证△AEF≌△AEN，从而将PE+EF转化为PE+EN，转化到（1）的情况，若BP＝3，AB＝6，AP＝3，则PE+EF的最小值为　 　；

（3）请应用以上转化思想解决问题（3），在直角△ABC中，∠C＝90°，∠B＝30°，AC＝10，点D是CD边上的动点，连接AD，将线段AD顺时针旋转60°，得到线段AP，连接CP，求线段CP的最小值．

Answer 1

【答案】（1）3；（2）；（3）PC的最小值为5．

【解析】

（1）如图1中，作AH⊥BC于H．根据垂线段最短，求出AH即可解决问题．

（2）如图2中，在AB上截取AN，使得AN＝AF，连接NE．作PH⊥AB于H．由△EAN≌△EAF（SAS），推出EN＝EF，推出PE+EF＝PE+NE，推出当P，E，N共线且与PH重合时，PE+PF的值最小，最小值为线段PH的长．

（3）如图3中，在AB上取一点K，使得AK＝AC，连接CK，DK．由△PAC≌△DAK（SAS），推出PC＝DK，易知KD⊥BC时，KD的值最小，求出KD的最小值即可解决问题．

解：（1）如图1中，作AH⊥BC于H．

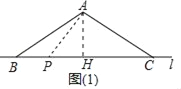
∵AB＝AC＝6，AH⊥BC，

∴∠BAH＝∠CAH＝∠BAC＝60°，

∴AH＝ABcos60°＝3，

根据垂线段最短可知，当AP与AH重合时，PA的值最小，最小值为3．

故答案为3．

（2）如图2中，在AB上截取AN，使得AN＝AF，连接NE．作PH⊥AB于H．

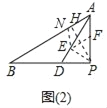
∵∠EAN＝∠EAF，AN＝AF，AE＝AE，

∴△EAN≌△EAF（SAS），

∴EN＝EF，

∴PE+EF＝PE+NE，

∴当P，E，N共线且与PH重合时，PE+PF的值最小，最小值为线段PH的长，

∵ABPH＝PAPB，

∴PH＝＝，

∴PE+EF的最小值为．

故答案为．

（3）如图3中，在AB上取一点K，使得AK＝AC，连接CK，DK．

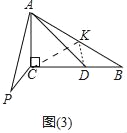
∵∠ACB＝90°，∠B＝30°，

∴∠CAK＝60°，

∴∠PAD＝∠CAK，

∴∠PAC＝∠DAK，

∵PA＝DA，CA＝KA，

∴△PAC≌△DAK（SAS），

∴PC＝DK，

∵KD⊥BC时，KD的值最小，最小值为5，

∴PC的最小值为5．