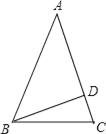
【题目】在等腰△ABC中,已知AB=AC,BD⊥AC于D.
(1)若∠A=48°,求∠CBD的度数;
(2)若BC=15,BD=12,求AB的长.
参考答案:
【答案】(1)∠CBD=24°;(2)AB=![]() .
.
【解析】
(1)根据等腰三角形的性质和直角三角形的两个锐角互余,可以求得∠CBD的度数;
(2)根据题目中的数据和勾股定理,可以求得AB的长.
解:(1)∵在等腰△ABC中,AB=AC,BD⊥AC,
∴∠ABC=∠C,∠ADB=90°,
∵∠A=48°,
∴∠ABC=∠C=66°,∠ABD=42°,
∴∠CBD=24°;
(2)∵BD⊥AC,
∴∠BDC=90°,
∵BC=15,BD=12,
∴CD=9,
设AB=x,则AD=x﹣9,
∵∠ADB=90°,BD=12,
∴122+(x﹣9)2=x2,
解得,x=![]() ,
,
即AB=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,下面四个结论:①CF=2AF;②tan∠CAD=
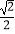 ;
;
③DF=DC;④△AEF∽△CAB;⑤ S四边形CDEF= S△ABF ,其中正确的结论有( )
S△ABF ,其中正确的结论有( )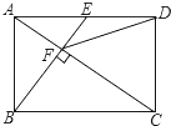
A.2个
B.3个
C.4个
D.5个 -
科目: 来源: 题型:
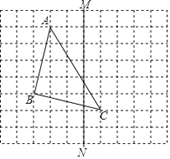
查看答案和解析>>【题目】如图,在长度为1个单位的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线MN成轴对称的△A1B1C1;(不写画法)
(2)请你判断△ABC的形状,并求出AC边上的高.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正△ABC的边长为2,过点B的直线l⊥AB,且△ABC与△A′BC′关于直线l对称,D为线段BC′上一动点,则AD+CD的最小值是( )
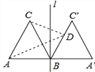
A. 4 B. 3
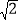 C. 2
C. 2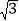 D. 2+
D. 2+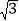
-
科目: 来源: 题型:
查看答案和解析>>【题目】某儿童游乐园门票价格规定如下表:
购票张数
1~50张
51~100张
100张以上
每张票的价格
13元
11元
9元
某校七年级(1)、(2)两个班共102人今年6.1儿童节去游该游乐园,其中(1)班人数较少,不足50人。经估算,如果两个班都以班为单位购票,则一共应付1218元。问:
(1)两个班各有多少学生?
(2)如果两班联合起来,作为一个团体购票,可以节省多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
 的图象经过点(﹣1,-2
的图象经过点(﹣1,-2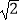 ),点A是该图象第一象限分支上的动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点D,当
),点A是该图象第一象限分支上的动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点D,当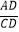 =
=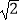 时,则点C的坐标为 .
时,则点C的坐标为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于平面内的∠M和∠N,若存在一个常数k>0,使得∠M+k∠N=360°,则称∠N为∠M的k系补周角.如若∠M=90°,∠N=45°,则∠N为∠M的6系补周角.


(1)若∠H=120°,则∠H的4系补周角的度数为 ;
(2)在平面内AB∥CD,点E是平面内一点,连接BE,DE.
①如图1,∠D=60°,若∠B是∠E的3系补周角,求∠B的度数;
②如图2,∠ABE和∠CDE均为钝角,点F在点E的右侧,且满足∠ABF=n∠ABE,∠CDF=n∠CDE(其中n为常数且n>1),点P是∠ABE角平分线BG上的一个动点,在P点运动过程中,请你确定一个点P的位置,使得∠BPD是∠F的k系补周角,并直接写出此时的k值(用含n的式子表示).
相关试题

