【题目】如图,在ABCD中,E,F分别为边AB,CD的中点,连接DE、BF、BD.

(1)求证:△ADE≌△CBF.
(2)若AD⊥BD,则四边形BFDE是什么特殊四边形?请证明你的结论.
参考答案:
【答案】(1)证明见解析;(2)菱形,证明见解析
【解析】
试题分析:(1)根据题中已知条件不难得出,AD=BC,∠A=∠C,E、F分别为边AB、CD的中点,那么AE=CF,这样就具备了全等三角形判定中的SAS,由此可得出△AED≌△CFB.
(2)直角三角形ADB中,DE是斜边上的中线,因此DE=BE,又由DE=BF,FD∥BE那么可得出四边形BFDE是个菱形.
(1)证明:在平行四边形ABCD中,∠A=∠C,AD=BC,
∵E、F分别为AB、CD的中点,
∴AE=CF.
在△ADE和△CBF中,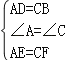
∴△ADE≌△CBF(SAS);
(2)解:若AD⊥BD,则四边形BFDE是菱形.
证明:∵AD⊥BD,
∴△ABD是直角三角形,且∠ADB=90°.
∵E是AB的中点,
∴DE=![]() AB=BE.
AB=BE.
∵在ABCD中,E,F分别为边AB,CD的中点,
∴EB∥DF且EB=DF,
∴四边形BFDE是平行四边形.
∴四边形BFDE是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把以 (-2,7),(-2,2)为端点的线段向右平移7个单位,所得像上任意一点的坐标可表示为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
某车间有32名工人,每人每天可加工甲种零件10个或乙种零件8个。在这32名工人中,一部分工人加工甲种零件,其余的加工乙种零件,已知每加工一个甲种零件可获利35元,每加工一个乙种零件可获利50元。若此车间这一天一共获利12200元,求这一天加工乙种零件工人的人数。
-
科目: 来源: 题型:
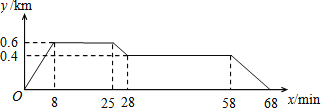
查看答案和解析>>【题目】如图反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,然后回家.其中x表示时间,y表示小明离家的距离,小明家、食堂、图书馆在同一直线上.根据图中提供的信息,有下列说法:
(1)食堂离小明家0.4km;
(2)小明从食堂到图书馆用了3min;
(3)图书馆在小明家和食堂之间;
(4)小明从图书馆回家的平均速度是0.04km/min.
其中正确的有( )
A.4个 B.3个 C.2个 D.1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种服装平均每天可以销售20件,每件盈利32元,在每件降价幅度不超过10元的情况下,若每件降价1元,则每天可多售出5件,若每天要盈利900元,每件应降价 元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a+b=-1,则a2+b2+2ab的值为 ( )
A. 1 B. -1 C. 3 D. -3
-
科目: 来源: 题型:
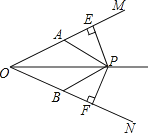
查看答案和解析>>【题目】如图,OP平分∠MON,PE⊥OM于E,PF⊥ON于F,OA=OB,则图中有 对全等三角形.
相关试题

