【题目】小红和小明在研究一个数学问题:已知AB∥CD,AB和CD都不经过点E,探索∠E与∠A,∠C的数量关系. 
(1)发现:在图1中,小红和小明都发现:∠AEC=∠A+∠C; 小红是这样证明的:如图7过点E作EQ∥AB.
∴∠AEQ=∠A()
∵EQ∥AB,AB∥CD.
∴EQ∥CD()
∴∠CEQ=∠C
∴∠AEQ+∠CEQ=∠A+∠C 即∠AEC=∠A+∠C.
小明是这样证明的:如图7过点E作EQ∥AB∥CD.
∴∠AEQ=∠A,∠CEQ=∠C
∴∠AEQ+∠CEQ=∠A+∠C即∠AEC=∠A+∠C
请在上面证明过程的横线上,填写依据:
两人的证明过程中,完全正确的是 .
(2)尝试: ①在图2中,若∠A=110°,∠C=130°,则∠E的度数为;
②在图3中,若∠A=20°,∠C=50°,则∠E的度数为 .
(3)探索: 装置图4中,探索∠E与∠A,∠C的数量关系,并说明理由.
(4)猜想: 如图5,∠B、∠D、∠E、∠F、∠G之间有什么关系?(直接写出结论)
(5)如图6,你可以得到什么结论?(直接写出结论)
参考答案:
【答案】
(1)两直线平行,内错角相等;平行于同一直线的两直线平行;小红的证法
(2)120°;30°
(3)解:∠E=∠A﹣∠C.
理由:延长EA,交CD于点F.
∵AB∥CD,
∴∠EFD=∠EAB
∵∠EFD=∠C+∠E
∴∠EAB=∠C+∠E
∴∠E=∠EAB﹣∠C.
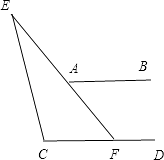
(4)解:可通过过点E、F、G分别做AB的平行线,得到结论.
∠E+∠G=∠B+∠F+∠D
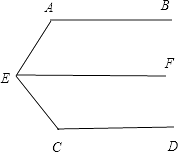
(5)解:同上道理一样,可得到结论:∠E1+∠E2+…+∠En=∠F1+∠F2+…∠Fn﹣1+∠B+∠D.
【解析】解:(1.)∵小明的辅助线做不出来,所以两人的证明过程中,小红的完全正确;答案:两直线平行,内错角相等;平行于同一直线的两直线平行;小红的证法. (2.)①过点E作EF∥AB,
∵AB∥CD,
∴EF∥CD.∵EF∥AB,
∴∠A+∠AEF=180°,
∵∠A=110°,∴∠AEF=70°.
∵EF∥CD,
∴∠C+∠CEF=180°,
∵∠C=130°,∴∠CEF=50°.
②∵AB∥CD,
∴∠EOB=∠C=50°
∵∠EOB=∠A+∠E,
∵∠E=∠EOB﹣∠A=50°﹣20°=30°.
答案:120°,30°.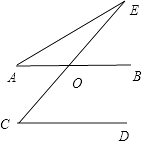
【考点精析】根据题目的已知条件,利用平行线的判定与性质的相关知识可以得到问题的答案,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1是一种可折叠台灯,它放置在水平桌面上,将其抽象成图2,其中点B,E,D均为可转动点.现测得AB=BE=ED=CD=15cm,经多次调试发现当点B,E所在直线垂直经过CD的中点F时(如图3所示)放置较平稳.
(1)求平稳放置时灯座DC与灯杆DE的夹角的大小;
(2)为保护视力,写字时眼睛离桌面的距离应保持在30cm,为防止台灯刺眼,点A离桌面的距离应不超过30cm,求台灯平稳放置时∠ABE的最大值.(结果精确到0.01°,参考数据:
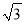 ≈1.732,sin7.70°≈0.134,cos82.30°≈0.134,可使用科学计算器)
≈1.732,sin7.70°≈0.134,cos82.30°≈0.134,可使用科学计算器)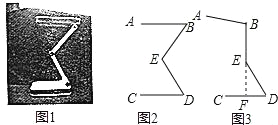
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,若点A在第一象限,则点A关于原点的中心对称点在( )
A.第一象限B.第二象限C.第三象限D.第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店需要购进甲、乙两种商品共180件,其进价和售价如表:(注:获利=售价﹣进价)
甲
乙
进价(元/件)
14
35
售价(元/件)
20
43
(1)若商店计划销售完这批商品后能获利1240元,问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于5040元,且销售完这批商品后获利多于1312元,请问有哪几种购货方案?并直接写出其中获利最大的购货方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】某天的最高气温是5℃,最低气温是﹣4℃,则这一天气温的温差是( )
A.1℃
B.﹣1℃
C.9℃
D.﹣9℃ -
科目: 来源: 题型:
查看答案和解析>>【题目】手机微信推出了抢红包游戏,它有多种玩法,其中一种为“拼手气红包”:用户设定好总金额以及红包个数后,可以生成不等金额的红包.现有一用户发了三个“拼手气红包”,随机被甲、乙、丙三人抢到.
(1)以下说法中正确的是
A.甲、乙两人抢到的红包金额之和一定比丙抢到的红包金额多
B.甲一定抢到金额最多的红包
C.乙一定抢到金额居中的红包
D.丙不一定抢到金额最少的红包
(2)记金额最多、居中、最少的红包分别为A,B,C,试求出甲抢到红包A的概率P(A).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个四边形中,如果有两个内角是直角,那么另外两个内角( ).
A. 都是钝角 B. 都是锐角
C. 一个是锐角,一个是直角 D. 互为补角
相关试题

