搜索
【题目】某校有21名同学们参加某比赛，预赛成绩各不同，要取前11名参加决赛，小颖已经知道了自己的成绩，她想知道自己能否进入决赛，只需要再知道这21名同学成绩的（ ）
A.最高分
B.中位数
C.极差
D.平均数
参考答案：
【答案】B
【解析】解：共有21名学生参加预赛，取前11名，所以小颖需要知道自己的成绩是否进入前11．我们把所有同学的成绩按大小顺序排列， 第11名的成绩是这组数据的中位数，所以小颖知道这组数据的中位数，才能知道自己是否进入决赛．
故选：B．
由于有21名同学参加百米竞赛，要取前11名参加决赛，故应考虑中位数的大小．
-
科目： 来源： 题型：
查看答案和解析>>【题目】潼南绿色无公害蔬菜基地有甲、乙两种植户，他们种植了A、B两类蔬菜，两种植户种植的两类蔬菜的种植面积与总收入如下表：
种植户
种植A类蔬菜面积
（单位：亩）种植B类蔬菜面积
（单位：亩）总收入
（单位：元）甲
3
1
12500
乙
2
3
16500
说明：不同种植户种植的同类蔬菜每亩平均收入相等．
（1）求A、B两类蔬菜每亩平均收入各是多少元？
（2）某种植户准备租20亩地用来种植A、B两类蔬菜，为了使总收入不低于63000元，且种植A类蔬菜的面积多于种植B类蔬菜的面积（两类蔬菜的种植面积均为整数），求该种植户所有租地方案． -
科目： 来源： 题型：
查看答案和解析>>【题目】某兴趣小组为了解我市气温变化情况，记录了今年月份连续
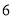天的最低气温（单位：℃）：
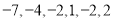.关于这组数据，下列结论不正确的是（ ）A．平均数是
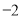B．中位数是
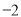C.众数是
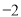D．方差是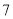
-
科目： 来源： 题型：
查看答案和解析>>【题目】综合：
（1）在四边形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°，E、F分别是BC、CD上的点，且∠EAF=60°，试探究图1中线段BE、EF、FD之间的数量关系． 小亮同学认为：延长FD到点G，使DG=BE，连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，则可得到BE、EF、FD之间的数量关系．请你按照小亮的思路写出推理过程．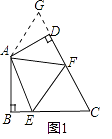
（2）如图2，已知正方形ABCD，△AEF是正方形ABCD的内接等边三角形，请你找出S△ABE、S△ADF、S△CEF之间的数量关系，并说明理由．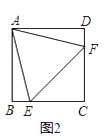
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列各式能用平方差公式计算的是（ ）
A.（2a+b）（2b﹣a）
B.（x+1）（﹣x﹣1）
C.（﹣m﹣n）（﹣m+n）
D.（3x﹣y）（﹣3x+y） -
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，点P（﹣20，a）与点Q（b，13）关于原点对称，则a+b的值为（ ）
A.33
B.﹣33
C.﹣7
D.7 -
科目： 来源： 题型：
查看答案和解析>>【题目】生物具有遗传多样性，遗传信息大多储存在DNA分子上．一个DNA分子的直径约为0.0000002cm，这个数量用科学记数法可表示为2×10ncm，则n= ．
相关试题
