【题目】已知:在平面直角坐标系xOy中,抛物线y=ax2+bx+c经过点A(3,0),B(2,﹣3),C(0,﹣3)
(1)求抛物线的表达式;
(2)设点D是抛物线上一点,且点D的横坐标为﹣2,求△AOD的面积.
参考答案:
【答案】(1)y=x2﹣2x﹣3;(2)![]() .
.
【解析】
试题分析:(1)把A,B,C三点坐标代入解析式求出a,b,c的值,即可求出函数解析式;
(2)把x=﹣2代入抛物线解析式求出y的值,确定出D坐标,由OA为底,D纵坐标绝对值为高,求出三角形AOD面积即可.
试题解析:(1)把A(3,0),B(2,﹣3),C(0,﹣3)代入y=ax2+bx+c得: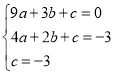
,解得: ,则抛物线解析式为y=x2﹣2x﹣3;
,则抛物线解析式为y=x2﹣2x﹣3;
(2)把x=﹣2代入抛物线解析式得:y=5,即D(﹣2,5),∵A(3,0),即OA=3,∴S△AOD=![]() ×3×5=
×3×5=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(2,﹣5)到x轴、y轴的距离分别为( )
A. 2、5 B. 2、﹣5 C. 5、2 D. ﹣5、2
-
科目: 来源: 题型:
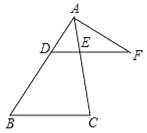
查看答案和解析>>【题目】如图,在△ABC中,点D是AB边上一点,过点D作DE∥BC,交AC于E,点F是DE延长线上一点,联结AF.
(1)如果
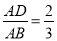 ,DE=6,求边BC的长;
,DE=6,求边BC的长;(2)如果∠FAE=∠B,FA=6,FE=4,求DF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正八边形的每个外角为_________度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,表示甲、乙两人沿同一条路长跑,两人的行程y(千米)与时间x(时)变化的图象(全程)如图所示,根据图象回答问题:

(1)乙的速度为千米/小时;两人是否同时到达终点(填“是”或“不是”);
(2)甲第一段的速度为千米/时;第二段的速度为千米/时;
(3)b、c表示的数字分别为、;
(4)若两人在相遇后1小时乙到达终点,则a表示的数字为;甲的行程是千米,乙的行程是千米. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的一个内角是100°,则它的底角是______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中,正确的是( )
A. (﹣x)2x3=x5B. (x2y)3=x6y
C. (a+b)2=a2+b2D. a6+a3=a2
相关试题

