搜索
【题目】某地某月1～20日中午12时的气温(单位：℃)如下：
22 31 25 15 18 23 21 20 27 17
20 12 18 21 21 16 20 24 26 19
(1)将下列频数分布表补充完整：
气温分组(℃) | 划记 | 频数 |
12≤x＜17 |
| 3 |
17≤x＜22 | ________ | _______ |
22≤x＜27 | _________ | ________ |
27≤x＜32 |
| 2 |
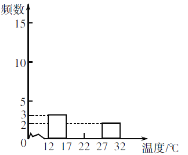
(2)补全频数分布直方图；
(3)根据频数分布表或频数分布直方图，分析数据的分布情况．
参考答案：
【答案】(1)正正；正；10；5；(2)补图见解析；(3)17℃≤x＜22℃时天数最多，有10天．
【解析】
依题意由表格数据来补全频数直方图，一一解答即可.
(1)正正 正 10 5
(2)补全频数分布直方图如下：
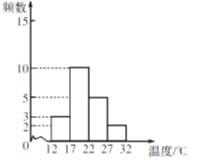
(3)由频数分布直方图知，17℃
x
22℃时天数最多，有10天．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校为了了解九年级学生的体能情况，抽调了一部分学生进行一分钟跳绳测试，将测试成绩整理后作出如图所示的统计图. 甲同学计算出前两组的频率和是0.12，乙同学计算出跳绳次数不少于100次的同学占96%，丙同学计算出从左至右第二、三、四组的频数的比为4∶17∶15，则本次测试共抽调的人数为( )
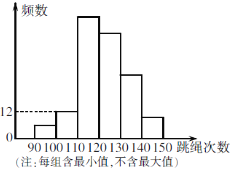
A. 120 B. 150 C. 180 D. 无法确定
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AD是∠BAC的平分线，AD的垂线平分线交AB于点F，交BC的延长线于点E，连接AE，DF.
求证：（1）∠EAD=∠EDA；（2）DF//AC；（3）∠EAC=∠B.
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了了解某地九年级学生参加消防知识竞赛成绩(均为整数)，从中抽取了1%的同学的竞赛成绩，整理后绘制了如下的频数直方图，请结合图形解答下列问题：
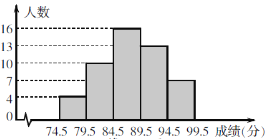
(1)这个问题中的总体是________________；
(2)竞赛成绩在84.5～89.5分这一小组的频率是_____________；
(3)若竞赛成绩在90分以上(含90分)的同学可以获得奖励，则估计该地获得奖励的九年级学生约有_____人．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，∠ECF＝90°，线段 AB 的端点分别在 CE 和 CF 上，BD 平分∠CBA，并与∠CAB 的外角平分线 AG 所在的直线交于一点 D．
（1）∠D 与∠C 有怎样的数量关系？（直接写出关系及大小）
（2）点 A 在射线 CE 上运动，（不与点 C 重合）时，其它条件不变，（1）中结论还成立吗？说说你的理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，经过点A（0，6）的抛物线y=
x2+bx+c与x轴相交于B（﹣2，0）、C两点．
（1）求此抛物线的函数关系式和顶点D的坐标；
（2）求直线AC所对应的函数关系式；
（3）将（1）中求得的抛物线向左平移1个单位长度，再向上平移m（m＞0）个单位长度得到新抛物线y1 ， 若新抛物线y1的顶点P在△ABC内，求m的取值范围；
（4）在（3）的结论下，新抛物线y1上是否存在点Q，使得△QAB是以AB为底边的等腰三角形，请分析所有可能出现的情况，并直接写出相对应的m的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC 中，BC＝AC，∠BCA＝90°，P 为直线 AC 上一点，过 A作 AD⊥BP 于 D，交直线 BC 于 Q．
(1)如图 1，当 P 在线段 AC 上时，求证：BP＝AQ．
(2)当 P 在线段 AC 的延长线上时，请在图 2 中画出图形，并求∠CPQ．
(3)如图 3，当 P 在线段 AC 的延长线上时，∠DBA＝ 时，AQ＝2BD．
相关试题
