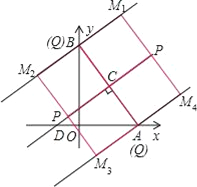
【题目】如图,在平面直角坐标系中,已知Rt△AOB的两直角边OA、OB分别在x轴、y轴的正半轴上(OA<OB),且OA、OB的长分别是一元二次方程x2﹣14x+48=0的两个根.线段AB的垂直平分线CD交AB于点C,交x轴于点D,点P是直线CD上一个动点,点Q是直线AB上一个动点.
(1)求A、B两点的坐标;
(2)求直线CD的解析式;
(3)在坐标平面内是否存在点M,使以点C、P、Q、M为顶点的四边形是正方形,且该正方形的边长为![]() AB长?若存在,请直接写出点M的坐标;若不存在,请说明理由.
AB长?若存在,请直接写出点M的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)A(6,0),B(0,8);
(2)y=![]() x+
x+![]() ;
;
(3)存在,M1(4,11),M2(﹣4,5),M3(2,﹣3),M4(10,3)
【解析】【试题分析】(1)利用因式分解法解方程x2﹣14x+48=0,求出x的值,即可得到A、B两点的坐标;
(2)先在Rt△AOB中利用勾股定理求出AB=![]() =10,根据线段垂直平分线的性质得到AC=
=10,根据线段垂直平分线的性质得到AC=![]() AB=5.再由两角对应相等的两三角形相似证明△ACD∽△AOB,由相似三角形对应边成比例得出
AB=5.再由两角对应相等的两三角形相似证明△ACD∽△AOB,由相似三角形对应边成比例得出![]() ,求出AD=
,求出AD=![]() ,得到D点坐标(﹣
,得到D点坐标(﹣![]() ,0),根据中点坐标公式得出C(3,4),然后利用待定系数法即可求出直线CD的解析式;
,0),根据中点坐标公式得出C(3,4),然后利用待定系数法即可求出直线CD的解析式;
(3)分两种情况进行讨论:①当点Q与点B重合时,先求出BM的解析式为y=![]() x+8,设M(x,
x+8,设M(x, ![]() x+8),再根据BM=5列出方程(
x+8),再根据BM=5列出方程(![]() x+8﹣8)2+x2=52,解方程即可求出M的坐标;②当点Q与点A重合时,先求出AM的解析式为y=
x+8﹣8)2+x2=52,解方程即可求出M的坐标;②当点Q与点A重合时,先求出AM的解析式为y=![]() x﹣
x﹣![]() ,设M(x,
,设M(x, ![]() x﹣
x﹣![]() ),再根据AM=5列出方程(
),再根据AM=5列出方程(![]() x﹣
x﹣![]() )2+(x﹣6)2=52,解方程即可求出M的坐标.
)2+(x﹣6)2=52,解方程即可求出M的坐标.
【试题解析】
(1)解方程x2﹣14x+48=0,
得x1=6,x2=8,
∵OA<OB,
∴A(6,0),B(0,8);
(2)在Rt△AOB中,∵∠AOB=90°,OA=6,OB=8,
∴AB=![]() =10,
=10,
∵线段AB的垂直平分线CD交AB于点C,
∴AC=![]() AB=5.
AB=5.
在△ACD与△AOB中,
![]() ,
,
∴△ACD∽△AOB,
∴![]() ,即
,即![]() ,
,
解得AD=![]() ,
,
∵A(6,0),点D在x轴上,
∴D(﹣![]() ,0).
,0).
设直线CD的解析式为y=kx+b,
由题意知C为AB中点,
∴C(3,4),
∵D(﹣![]() ,0),
,0),
∴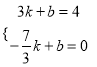 ,解得
,解得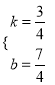 ,
,
∴直线CD的解析式为y=![]() x+
x+![]() ;
;
(3)在坐标平面内存在点M,使以点C、P、Q、M为顶点的四边形是正方形,且该正方形的边长为![]() AB长.
AB长.
∵AC=BC=![]() AB=5,
AB=5,
∴以点C、P、Q、M为顶点的正方形的边长为5,且点Q与点B或点A重合.分两种情况:
当点Q与点B重合时,易求BM的解析式为y=![]() x+8,设M(x,
x+8,设M(x, ![]() x+8),
x+8),
∵B(0,8),BM=5,
∴(![]() x+8﹣8)2+x2=52,
x+8﹣8)2+x2=52,
化简整理,得x2=16,
解得x=±4,
∴M1(4,11),M2(﹣4,5);
当点Q与点A重合时,易求AM的解析式为y=![]() x﹣
x﹣![]() ,设M(x,
,设M(x, ![]() x﹣
x﹣![]() ),
),
∵A(6,0),AM=5,
∴(![]() x﹣
x﹣![]() )2+(x﹣6)2=52,
)2+(x﹣6)2=52,
化简整理,得x2﹣12x+20=0,
解得x1=2,x2=10,
∴M3(2,﹣3),M4(10,3);
综上所述,所求点M的坐标为M1(4,11),M2(﹣4,5),M3(2,﹣3),M4(10,3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=( )
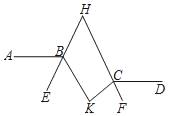
A. 76° B. 78° C. 80° D. 82°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,,点D是边AB上一点,E为AC的中点,过点C作CF∥AB, 交DE的延长线于点F。
(1)求证:DE=FE;
(2)若CD=CF,∠A=40°,求∠BCD的度数。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,已知正比例函数y=
 x的图象与反比例函数y=
x的图象与反比例函数y= 的图象交于A(a,-2),B两点.
的图象交于A(a,-2),B两点.(1)求反比例函数的表达式和点B的坐标;
(2)P是第一象限内反比例函数图象上一点,过点P作y轴的平行线,交直线AB于点C,连接PO,若△POC的面积为3,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在宽20米,长32米的矩形耕地上,修筑同样宽的三条路(两条纵向,一条横向,并且横向与纵向互相垂直),把这块耕地分成大小相等的六块试验田,要使试验田的面积是570平方米,问道路应该多宽?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD的外侧,作等边
 ADE,则
ADE,则 BED的度数是 .
BED的度数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线AB和CD相交于点O,在∠COB的内部作射线OE.
(1)若∠AOC=36°,∠COE=90°,求∠BOE的度数;
(2)若∠COE:∠EOB:∠BOD=4:3:2,求∠AOE的度数.
相关试题

