【题目】学校科技小组研制了一套信号发射、接收系统.在对系统进行测试中,如图,小明从路口A处出发,沿东南方向笔直公路行进,并发射信号,小华同时从A处出发,沿西南方向笔直公路行进,并接收信号.若小明步行速度为39米/分,小华步行速度为52米/分,恰好在出发后30分时信号开始不清晰.
(1)你能求出他们研制的信号收发系统的信号传送半径吗?(以信号清晰为界限)
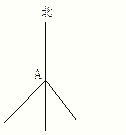
(2)通过计算,你能找到题中数据与勾股数3、4、5的联系吗?试从中寻找求解决问题的简便算法.
参考答案:
【答案】(1)1950米;(2)详见解析.
【解析】试题分析:
(1)设30分钟时,小明刚好到达C处,小华刚好到达B处,连接BC,则由已知易得AC=![]() ,AB=
,AB=![]() ,∠BAC=90°,由勾股定理在Rt△ABC中计算出BC的长就可得收发系统的传送半径;
,∠BAC=90°,由勾股定理在Rt△ABC中计算出BC的长就可得收发系统的传送半径;
(2)由(1)可知:数据![]() 是一组勾股数,而
是一组勾股数,而![]() ,由此可知勾股数“3、4、5”的整数倍也是一组“勾股数”,这样我们就可以直接由“
,由此可知勾股数“3、4、5”的整数倍也是一组“勾股数”,这样我们就可以直接由“![]() ”来计算本题第(1)问中的传送半径了.
”来计算本题第(1)问中的传送半径了.
试题解析:
(1)如图,设30分钟时,小明刚好到达C处,小华刚好到达B处,连接BC,则由已知易得AC=![]() ,AB=
,AB=![]() ,∠BAC=90°,
,∠BAC=90°,
∴BC=![]() (米),即信号传送半径为1950米;
(米),即信号传送半径为1950米;
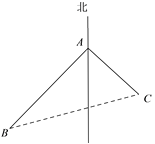
(2)∵小明所走的路程为39×30=3×13×30,小华所走的路程为52×30=4×13×30,30分钟时,两人间的距离为: ![]() ,
,
∴结合(1)可知勾股数3、4、5的倍数仍能构成一组勾股数,
∴可用5×13×30=1950(米)来计算传送半径,这样比用勾股定理计算要简单一些.
-
科目: 来源: 题型:
查看答案和解析>>【题目】求下列各式中x的值.
(1)x2=5
(2)x2﹣5=
(3)(x﹣2)2=125
(4)(y+3)3+64=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知△ABC与△CDA关于点O对称,过O任作直线EF分别交AD、BC于点E、F,下面的结论:
①点E和点F,点B和点D是关于中心O对称点;
②直线BD必经过点O;
③四边形DEOC与四边形BFOA的面积必相等;
④△AOE与△COF成中心对称.
其中正确的个数为( )

A.1 B.2 C.3 D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=2x-3,若自变量x的取值范围是-1≤x≤3,则函数值y的取值范围是( )
A. -5≤y≤3 B. -4≤y≤5 C. 1≤y≤9 D. -1≤y≤3
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面推理过程:
如图,已知DE∥BC,DF、BE分别平分∠ADE、∠ABC,可推得∠FDE=∠DEB的理由:
∵DE∥BC(已知)
∴∠ADE= .( )
∵DF、BE分别平分∠ADE、∠ABC,
∴∠ADF=
∠ABE= .( )
.( )
∴∠ADF=∠ABE
∴DF∥ .()
∴∠FDE=∠DEB.( )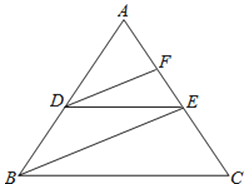
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)四年一度的国际数学家大会于2002年8月20日在北京召开,大会会标如图8,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积为13,每个直角三角形两直角边的和是5,求中间小正方形的面积.
(2)现有一张长为6.5cm,宽为2cm的纸片,如图9,请你将它分割成6块,再拼合成一个正方形.(要求:先在图9中画出分割线,再画出拼成的正方形并标明相应数据)


-
科目: 来源: 题型:
查看答案和解析>>【题目】H7N9时一种新型禽流感,其病毒颗粒呈多形性,其中球形病毒的最大直径为0.00000012米,这一直径用科学记数法表示为( )
A.1.2×10﹣7米
B.1.2×10﹣8米
C.12×10﹣8米
D.12×10﹣9米
相关试题

