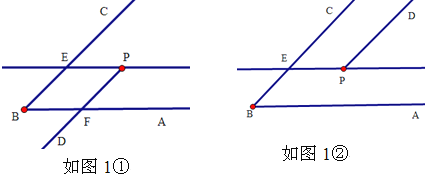
【题目】(1)如图1,P是∠ABC内一点,请过点P画射线PD,使PD∥BC;过点P画直线PE∥BA,交BC于点E.请画图并通过观察思考后你发现∠ABC与∠DPE的大小关系是 ,并说明理由.
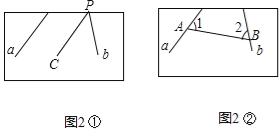
(2)如图2,直线a,b所成的角跑到画板外面去了,为了测量这两条直线所成的角的度数,请画图并简单地写出你的方法.

参考答案:
【答案】(1)相等或互补 (2)见解析
【解析】试题分析:(1)分两种情况讨论;(2)利用平行线的性质或三角形的内角和设计方法.
试题解析:(1)相等或互补
理由如下:
如图1①,
DP交AB于点F.
∵PD∥BC,
∴∠ABC=∠AFP,
∵PE∥BA,
∴∠AFP=∠DPE,
∴∠ABC=∠DPE;
如图1②,
设DP交AB于点F.
∵PD∥BC,
∴∠ABC=∠CEP,
∵PD∥BC,
∴∠CEP+∠DPE=180°,
∴∠ABC+∠DPE=180°;
(2)方法一:
如图2①,设直线b与木板交于点P,
过点P作PC∥a,量出直线b与PC的夹角度数,即为直线a,b所成角的度数,
依据是:两直线平行,同位角相等;
方法二:
如图2②,在直线a,b上各取一点A,B,
连结AB,测得∠1,∠2的度数,
则180°﹣∠1﹣∠2即为直线a,b所成角的度数;
依据是:三角形内角和为180°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC≌△DEC,△ABC的周长为100cm,DE=30cm,EC=25cm,那么BC长为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x(x﹣1)=x﹣1的解是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=
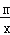 (m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.
(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.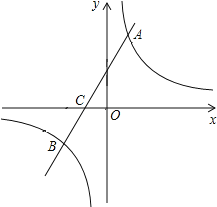
(1)求该反比例函数和一次函数的解析式;
(2)求点B的坐标;
(3)在x轴上求点E,使△ACE为直角三角形.(直接写出点E的坐标)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个角的补角是150°,那么这个角的余角的度数是( )
A、30° B、60° C、90° D、120°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个多边形的每一个外角都是45°,那么这个多边形的内角和是( )
A.540° B.720° C.1080° D.1260°
-
科目: 来源: 题型:
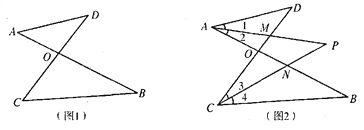
查看答案和解析>>【题目】试解答下列问题:
(1)在图1我们称之为“8字形”,请直接写出∠A、∠B、∠C、∠D之间的数量关系: ;
(2)仔细观察,在图2中“8字形”的个数是 个;
(3) 在图2中,若∠D=40°,∠B=36°,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试求∠P的度数;
(4)如果图2中∠D和∠B为任意角时,其他条件不变,试写出∠B与∠P、∠D之间数量关系 .
相关试题

