【题目】如图,三角形DEF是三角形ABC沿射线BC平移的得到的,BE=2,DE与AC交于点G,且满足DG=2GE.若三角形CEG的面积为1,CE=1,则点G到AD的距离为 . 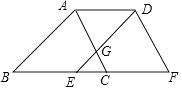
参考答案:
【答案】4
【解析】解:∵三角形DEF是三角形ABC沿射线BC平移的得到的,BE=2,∴AD=BE=2,
∵三角形CEG的面积为1,CE=1,
∴点G到CE的距离为2,
∵DG=2GE,
∴点G到AD的距离为4,
所以答案是:4
【考点精析】利用三角形的面积和平移的性质对题目进行判断即可得到答案,需要熟知三角形的面积=1/2×底×高;①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化;②经过平移后,对应点所连的线段平行(或在同一直线上)且相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一种药品经两次降价,由每盒50元调至40.5元,平均每次降价的百分率是( )
A.5%
B.10%
C.15%
D.20% -
科目: 来源: 题型:
查看答案和解析>>【题目】观察方程(x﹣1)(x+2)=0的解是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在实数范围定义运算“”:ab=2a+b,则满足x(x﹣6)=0的实数x是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个运算程序的示意图,若开始输入的x值为81,我们看到第一次输出的结果为27,第二次输出的结果为9,…,第2017次输出的结果为( )
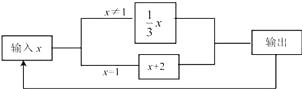
A.1
B.3
C.9
D.27 -
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD 中,AB=3,BC=4,E,F 是对角线 AC上的两个动点,分别从 A,C 同时出发, 相向而行,速度均为 1cm/s,运动时间为 t 秒,当其中一个动点到达后就停止运动.
(Ⅰ)若 G,H 分别是 AB,DC 中点,求证:四边形 EGFH 始终是平行四边形.
(Ⅱ)在(1)条件下,当 t 为何值时,四边形 EGFH 为矩形.
(Ⅲ)若 G,H 分别是折线 A﹣B﹣C,C﹣D﹣A 上的动点,与 E,F 相同的速度同时出发,当 t 为何值时,四边形 EGFH 为菱形.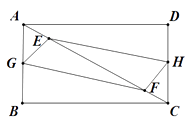
-
科目: 来源: 题型:
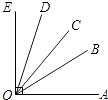
查看答案和解析>>【题目】如图所示,∠AOE=90°,∠BOD=45°,那么图中不大于90°的角有个,它们的度数之和是°.
相关试题

