【题目】已知,如图1:△ABC中,∠B、∠C的平分线相交于点O,过点O作EF∥BC交AB、AC于E、F.
(1)直接写出图1中所有的等腰三角形,并指出EF与BE、CF间有怎样的数量关系?
(2)在(1)的条件下,若AB=10,AC=15,求△AEF的周长.
(3)如图2,若△ABC中,∠B的平分线与三角形外角∠ACG的平分线CO交于点O,过O点作OE∥BC交AB于E,交AC于F,请问(1)中EF与BE、CF间的关系还是否存在,若存在,说明理由;若不存在,写出三者新的数量关系,并说明理由.
参考答案:
【答案】
(1)解:有2个等腰三角形分别是:等腰△OBE和等腰△OCF,
EF=BE+CF.
(2)解:△AEF的周长为AE+AF+EF=AE+AF+OE+OF=AE+AF+BE+CF=AB+AC=25
(3)解:(1)中EF与BE,CF间的关系不存在,新的数量关系为:EF=BE-CF,
证明:由BO平分∠ABC及OE∥BC可证BE=EO,
由CO平分∠ACG及OE∥BC可证CF=FO,
而EO=EF+OF,则EF=EO-OF=BE-CF
【解析】(1) 根据已知条件∠B、∠C的平分线相交于点O,及EF∥BC,可证得∠EBO=∠EOB,∠FCO=∠FOC,得出OE=BE,OF=FC,即可证得△OBE和△OCF是等腰三角形,及EF=BE+CF。
(2)由(1)可知EF=BE+CF,得出△AEF的周长=AB+AC,代入计算即可得出结果。
(3)根据已知条件可知新的数量关系为:EF=BE-CF,先证明BE=EO,CF=FO,再由EO=EF+OF,就可得出EF==BE-CF。
-
科目: 来源: 题型:
查看答案和解析>>【题目】自学下面材料后,解答问题.
分母中含有未知数的不等式叫做分式不等式.如: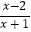 >0;
>0; 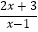 <0等.那么如何求出它们的解集呢?
<0等.那么如何求出它们的解集呢?
根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负.其字母表达式为:
(1)若a>0,b>0,则 >0;若a<0,b<0,则
>0;若a<0,b<0,则  >0;解不等式
>0;解不等式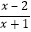 <0.
<0.
(2)若a>0,b<0,则 <0;若a<0,b>0,则
<0;若a<0,b>0,则  <0.
<0.
反之:①若 >0,则
>0,则 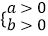 或
或 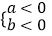 ,
,
②若 <0,则
<0,则 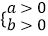 或
或 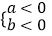 .
.
根据上述规律,①求不等式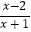 < 0的解集.
< 0的解集.
②直接写出不等式解集为x>3或x<1的最简分式不等式. -
科目: 来源: 题型:
查看答案和解析>>【题目】某青年旅社有60间客房供游客居住,在旅游旺季,当客房的定价为每天200元时,所有客房都可以住满.客房定价每提高10元,就会有1个客房空闲,对有游客入住的客房,旅社还需要对每个房间支出20元/每天的维护费用,设每间客房的定价提高了x元.
(1)填表(不需化简)
入住的房间数量
房间价格
总维护费用
提价前
60
200
60×20
提价后
(2)若该青年旅社希望每天纯收入为14000元且能吸引更多的游客,则每间客房的定价应为多少元?(纯收入=总收入﹣维护费用)
-
科目: 来源: 题型:
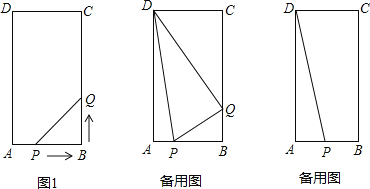
查看答案和解析>>【题目】在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以每秒1cm的速度移动,同时,点Q从点B出发沿BC边向点C以每秒2cm的速度移动.如果P、Q两点在分别到达B、C两点后就停止移动,回答下列问题:
(1)运动开始后第几秒时,△PBQ的面积等于8cm2?
(2)当运动开始后
 秒时,试判断△DPQ的形状;
秒时,试判断△DPQ的形状;(3)在运动过程中,是否存在这样的时刻,使以Q为圆心,PQ为半径的圆正好经过点D?若存在,求出运动时间;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:a2+a= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(2a2b)2的正确结果是( )
A.4a2b
B.2a4b2
C.4a4b2
D.2a4b -
科目: 来源: 题型:
查看答案和解析>>【题目】某轮船顺水航行3小时,逆水航行1.5小时,已知轮船在静水中的速度为a千米/时,水流速度为y千米/时,求轮船共航行多少千米?
相关试题

