搜索
【题目】已知抛物线的顶点坐标（2，3）且过点（3，4），求抛物线的解析式．
参考答案：
【答案】y＝（x﹣2）2+3
【解析】
已知了抛物线的顶点坐标，可用顶点式设抛物线的解析式，然后将点（3，4）代入抛物线的解析式中，即可求得待定系数法的值，也就求出了抛物线的解析式．
解：设抛物线的解析式为：y＝a（x﹣2）2+3，
∵（3，4）在抛物线y＝a（x﹣2）2+3上，
∴a（3﹣2）2+3＝4，
∴解得：a＝1，
∴此抛物线的解析式：y＝（x﹣2）2+3．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形ABCD中，AE=AB，直线DE交BC于点F，则∠BEF=度．
-
科目： 来源： 题型：
查看答案和解析>>【题目】请你从下列条件：①AB＝CD，②AD＝BC，③AB∥CD，④AD∥BC中任选两个，使它们能判定四边形ABCD是平行四边形．共有________种情况符合要求．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知一个二次函数的图象开口向上，顶点坐标为（2，3），那么这个二次函数的解析式可以是_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中A点的坐标为（8，y），AB⊥x轴于点B，sin∠OAB=
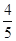，反比例函数y=
的图象的一支经过AO的中点C，且与AB交于点D．（1）求反比例函数解析式；
（2）若函数y=3x与y=
的图象的另一支交于点M，求三角形OMB与四边形OCDB的面积的比．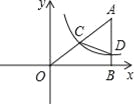
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，从地面上的点A看一山坡上的电线杆PQ，测得杆顶端点P的仰角是45°，向前走6m到达B点，测得杆顶端点P和杆底端点Q的仰角分别是60°和30°．
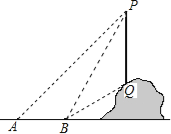
（1）求∠BPQ的度数；
（2）求该电线杆PQ的高度（结果精确到1m）．
备用数据：
，
． -
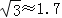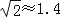科目： 来源： 题型：
查看答案和解析>>【题目】设集合A={x∈Z|（x+1）（x﹣4）=0}，B={x|x≤a}，若A∩B=A，则a的值可以是（ ）
A.1
B.2
C.3
D.4
相关试题
