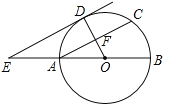
【题目】如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交![]() 于点D,过点D作⊙O的切线,交BA的延长线于点E.
于点D,过点D作⊙O的切线,交BA的延长线于点E.
(1)求证:AC∥DE;
(2)连接CD,若OA=AE=a,写出求四边形ACDE面积的思路.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)欲证明AC∥DE,只要证明AC⊥OD,ED⊥OD即可.
(2)作DM⊥OA于M,连接CD,CO,AD,首先证明四边形ACDE是平行四边形,根据S平行四边形ACDE=AEDM,只要求出DM即可.
试题解析:(1)∵ED与⊙O相切于D,∴OD⊥DE,∵F为弦AC中点,∴OD⊥AC,∴AC∥DE.
(2)作DM⊥OA于M,连接CD,CO,AD.
首先证明四边形ACDE是平行四边形,根据S平行四边形ACDE=AEDM,只要求出DM即可.
∵AC∥DE,AE=AO,∴OF=DF,∵AF⊥DO,∴AD=AO,∴AD=AO=OD,∴△ADO是等边三角形,同理△CDO也是等边三角形,∴∠CDO=∠DOA=60°,AE=CD=AD=AO=DD=a,∴AO∥CD,又AE=CD,∴四边形ACDE是平行四边形,易知DM=![]() ,∴平行四边形ACDE面积=
,∴平行四边形ACDE面积=![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】探索规律,观察下面算式,解答问题.
1+3 =4 =22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+7+9=25=52;
(1)请猜想1+3+5+7+9+…+19=
(2)请猜想1+3+5+7+9+…+(2n-1)+(2n +1)+(2n +3)=
(3)试计算:101 +103+…+197 +199.
-
科目: 来源: 题型:
查看答案和解析>>【题目】检修小组从A地出发,在东西路上检修线路,若规定向东行驶的路程为正数,向西行驶的路程为负数,一天中行驶记录(单位;千米)如下:
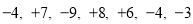
(1)收工时检修小组在A地的哪侧,距A地多远?
(2)若每千米耗油0.3升,从出发到收工共耗油多少升?
-
科目: 来源: 题型:
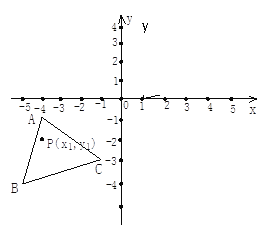
查看答案和解析>>【题目】如图, 已知A(-4,-1),B(-5,-4),C(-1,-3),△ABC经过平移得到的△A′B′C′,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4)。
(1)请在图中作出△A′B′C′;(2)写出点A′、B′、C′的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程(x+3)(x﹣4)=0的两个根为( )
A. x1=﹣2,x2=6B. x1=﹣6,x2=2C. x1=﹣3,x2=4D. x1=﹣4,x2=3
-
科目: 来源: 题型:
查看答案和解析>>【题目】两条纸带,较长的一条长23 cm,较短的一条长15 cm.把两条纸带剪下同样长的一段后,剩下的两条纸带中,要求较长的纸带的长度不少于较短的纸带长度的两倍,那么剪下的长度至少是( )
A.6 cm
B.7 cm
C.8 cm
D.9 cm -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,设△ABC的面积为S,周长为l.
(1)填表:
三边a、b、c
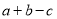
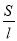
3、4、5
2
5、12、13
4
8、15、17
6
(2)如果
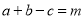 ,观察上表猜想:
,观察上表猜想: 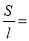 (用含有m的代数式表示).
(用含有m的代数式表示).(3)证明(2)中的结论.
相关试题

