【题目】已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA中点,点P在BC上以每秒1个单位的速度由C向B运动,设运动时间为t秒.

(1)△ODP的面积S=________.
(2)t为何值时,四边形PODB是平行四边形?
(3)在线段PB上是否存在一点Q,使得ODQP为菱形?若存在,求t的值,并求出Q点的坐标;若不存在,请说明理由;
(4)若△OPD为等腰三角形,请写出所有满足条件的点P的坐标(请直接写出答案,不必写过程)
参考答案:
【答案】(1)10;(2)5;(3)(8,4);(4)满足条件的点P的坐标为P1(3,4),P2(2.5,4),P3(2,4),P4(8,4).
【解析】
试题(1)根据三角形的面积公式即可求出△ODP的面积S;
(2)由于PB∥OD,根据平行四边形的判定可知当PB=OD=5时,四边形PODB是平行四边形,再求出PC=5,从而求出t的值;
(3)根据菱形的判定,当OD=OP=PQ=5时,四边形ODQP为菱形,在Rt△OPC中,利用勾股定理求出CP的值,进而求出t的值及Q点的坐标;
(4)当△OPD为等腰三角形时,分三种情况进行讨论:①如果O为顶点,那么OP=OD=5,②如果P为顶点,那么PO=PD,③如果D为顶点,那么DP=DO=5,分别做辅助线,利用勾股定理求出P点的坐标.
试题解析:(1)∵O为坐标原点,A(10,0),四边形OABC为矩形,C(0,4),
∴OA=BC=10,OC=4,
∵点D是OA中点,
∴OD=DA= ![]() OA=5,
OA=5,
∴△ODP的面积S= ![]() ODOC=
ODOC= ![]() ×5×4=10.
×5×4=10.
(2)解:∵PB∥OD,
∴当PB=OD时,四边形PODB是平行四边形,
∵OD=5,
∴PB=5,
∴PC=BC﹣PB=10﹣5=5,
∵点P在BC上以每秒1个单位的速度由C向B运动,
∴t=5
(3)解:当OD=OP=PQ=5时,ODQP为菱形,
在Rt△OPC中,由勾股定理得:
PC= ![]() =
= ![]() =3,
=3,
∴t=3,CQ=CP+PQ=3+5=8,
∴Q点的坐标为(8,4)
(4)解:△OPD为等腰三角形时,分三种情况:
①如果O为顶点,那么OP=OD=5,
由勾股定理可以求得PC=3,此时P1(3,4);
②如果P为顶点,那么PO=PD,
作PE⊥OA于E,则OE=ED=2.5,此时P2(2.5,4);
③如果D为顶点,那么DP=DO=5,
作DF⊥BC于F,由勾股定理,得PF=3,
∴P3C=5﹣3=2或P4C=5+3=8,此时P3(2,4),P4(8,4).
综上所述,满足条件的点P的坐标为P1(3,4),P2(2.5,4),P3(2,4),P4(8,4).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 ABCD中,E为对角线AC延长线上的一点.
ABCD中,E为对角线AC延长线上的一点.(1)若四边形ABCD是菱形,求证:BE=DE.
(2)写出(1)的逆命题,并判断其是真命题还是假命题,若是真命题,给出证明;若是假命题,举出反例.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(2015南通)如图,在ABCD中,点E,F分别在AB,DC上,且ED⊥DB,FB⊥BD.
(1)求证:△AED≌△CFB;
(2)若∠A=30°,∠DEB=45°,求证:DA=DF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是矩形,点E在CD边上,点F在DC延长线上,AE=BF.
(1)求证:四边形ABFE是平行四边形;
(2)若∠BEF=∠DAE,AE=3,BE=4,求EF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为了检验教室里的矩形门框是否合格,某班的四个学习小组用三角板和细绳分别测得如下结果,其中不能判定门框是否合格的是( )
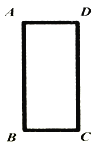
A. AB=CD,AD=BC,AC=BD B. AC=BD,∠B=∠C=90° C. AB=CD,∠B=∠C=90° D. AB=CD,AC=BD
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是
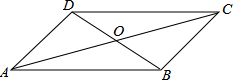
A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.

(1)求证:ED是⊙O的切线;
(2)当OE=10时,求BC的长.
相关试题

