【题目】如图,一圆与平面直角坐标系中的x轴切于点A(8,0),与y轴交于点B(0,4),C(0,16),则该圆的直径为。
参考答案:
【答案】20
【解析】过圆心O′作y轴的垂线,垂足为D,连接O′A,
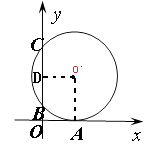
∵O′D⊥BC,
∴D为BC中点,
∴BC=16-4=12,OD=6+4=10,
∵⊙O′与x轴相切,
∴O′A⊥x轴,
∴四边形OAO′D为矩形,
半径O′A=OD=10,
∴直径是20.
【考点精析】利用垂径定理和切线的性质定理对题目进行判断即可得到答案,需要熟知垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】同时掷两枚标有数字1~6的正方形骰子,数字和为1的概率是 。
-
科目: 来源: 题型:
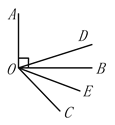
查看答案和解析>>【题目】如图,DO平分∠AOC,OE平分∠BOC,若OA⊥OB,
(1)当∠BOC=30°,∠DOE=_______________; 当∠BOC=60°,∠DOE=_______________;
(2)通过上面的计算,猜想∠DOE的度数与∠AOB有什么关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=2,BC=
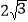 ,且∠BAC=120°,点D是线段BC上的一动点(不与点B、C重合),连接AD,作∠ADE=30°,DE交AC于点E.
,且∠BAC=120°,点D是线段BC上的一动点(不与点B、C重合),连接AD,作∠ADE=30°,DE交AC于点E.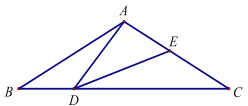
(1)求证:∠BAD∠EDC;
(2)当BD= 时,△ABD≌△EDC,并说明理由.
(3)当△ADE是直角三角形时,求AD的长?
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线
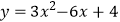 先向右平移3个单位长度,再向上平移2个单位长度后得到新的抛物线的顶点坐标为 .
先向右平移3个单位长度,再向上平移2个单位长度后得到新的抛物线的顶点坐标为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】若正整数
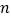 使得在计算
使得在计算 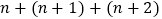 的过程中,各数位不产生进位现象,则称
的过程中,各数位不产生进位现象,则称 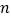 为“本位数.现从所有大于0,且小于100的“本位数”中,随机抽取一个数,抽到偶数的概率为= .
为“本位数.现从所有大于0,且小于100的“本位数”中,随机抽取一个数,抽到偶数的概率为= . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,那么DF∥AC,请完成它成立的理由
∵∠1=∠2,∠2=∠3 ,∠1=∠4( )
∴∠3=∠4( )
∴________∥_______ ( )
∴∠C=∠ABD( )
∵∠C=∠D( )
∴∠D=∠ABD( )
∴DF∥AC( )

相关试题

