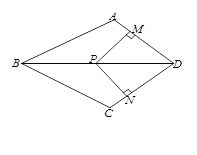
【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC, P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M、N.
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
参考答案:
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)根据角平分线的性质和全等三角形的判定方法证明△ABD≌△CBD,由全等三角形的性质即可得到:∠ADB=∠CDB;
(2)若∠ADC=90°,由(1)中的条件可得四边形MPND是矩形,再根据两边相等的四边形是正方形即可证明四边形MPND是正方形.
证明:(1)∵对角线BD平分∠ABC,
∴∠ABD=∠CBD,
在△ABD和△CBD中
AB=CB
∠ABD=∠CBD
BD=BD
∴△ABD≌△CBD(SAS)
∴∠ADB=∠CDB
(2)∵PM⊥AD,PN⊥CD,
∴∠PMD=∠PND=90,
∵∠ADC=90°,
∴四边形MPND是矩形,
∵∠ADB=∠CDB,
∴∠ADB=45°,
∴PM=MD,
∴四边形MPND是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某篮球运动员去年共参加40场比赛,其中3分球的命中率为0.25,平均每场有12次3分球未投中.
(1)该运动员去年的比赛中共投中多少个3分球?
(2)在其中的一场比赛中,该运动员3分球共出手20次,小亮说,该运动员这场比赛中一定投中了5个3分球,你认为小亮的说法正确吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】教室内的饮水机接通电源进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(分钟)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.如图为在水温为30℃时,接通电源后,水温y(℃)和时间x(分钟)的关系如图.
(1)a= ;
(2)直接写出图中y关于x的函数关系式;
(3)饮水机有多少时间能使水温保持在70℃及以上?
(4)若饮水机早上已加满水,开机温度是20℃,为了使8:40下课时水温达到70℃及以上,并节约能源,直接写出当它上午什么时间接通电源比较合适?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,三角形
 (记作
(记作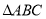 )在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是
)在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是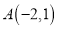 ,
,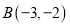 ,
,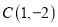 ,先将
,先将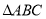 向上平移3个单位长度,再向右平移2个单位长度,得到
向上平移3个单位长度,再向右平移2个单位长度,得到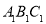 .
.
(1)在图中画出
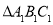 ;
;(2)点
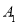 ,
,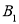 的坐标分别为______、______;
的坐标分别为______、______;(3)若
 轴有一点
轴有一点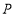 ,使
,使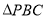 与
与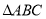 面积相等,求出
面积相等,求出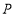 点的坐标.
点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边 ABC 的边长是 2 , D 、 E 分别为 AB 、 AC 的中点,连接CD ,过 E 点作 EF // DC 交 BC 的延长线于点 F
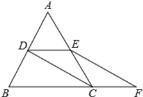
(1) 求证:四边形 CDEF 是平行四边形;
(2)求四边形 CDEF 的周长
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线
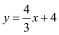 分别交
分别交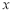 轴,
轴,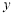 轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.
轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.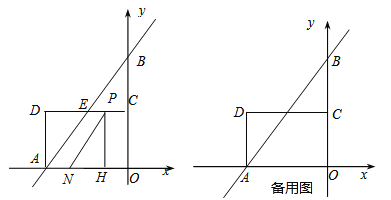
(1)直接写出点A,B的坐标,并求直线AB与CD交点E的坐标;
(2)动点P从点C出发,沿线段CD以每秒1个单位长度的速度向终点D运动;同时,动点N从点A出发,沿线段AO以每秒1个单位长度的速度向终点O运动,过点P作
 ,垂足为H,连接NP.设点P的运动时间为
,垂足为H,连接NP.设点P的运动时间为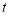 秒.
秒.①若△NPH的面积为1,求
 的值;
的值;②点Q是点B关于点A的对称点,问
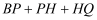 是否有最小值,如果有,求出相应的点P的坐标;如果没有,请说明理由.
是否有最小值,如果有,求出相应的点P的坐标;如果没有,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
(1)求证:△AEC≌△ADB;
(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.

相关试题

