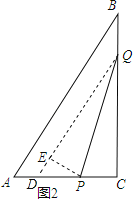
【题目】如图1,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,点P从A出发沿AC向C点以1厘米/秒的速度匀速移动;点Q从C出发沿CB向B点以2厘米/秒的速度匀速移动.点P、Q分别从起点同时出发,移动到某一位置时所需时间为t秒.

(1)当t=2时,求线段PQ的长度;
(2)当t为何值时,△PCQ的面积等于5cm2?
(3)在P、Q运动过程中,在某一时刻,若将△PQC翻折,得到△EPQ,如图2,PE与AB能否垂直?若能,求出相应的t值;若不能,请说明理由.
参考答案:
【答案】(1)![]() 厘米;(2)当t=1秒时,△PCQ的面积等于5cm2;(3)当t=
厘米;(2)当t=1秒时,△PCQ的面积等于5cm2;(3)当t=![]() 时,PE⊥AB.
时,PE⊥AB.
【解析】
试题分析:(1)当t=2时,可求出CP,CQ的长,根据勾股定理即可求出线段即斜边PQ的长;
(2)由三角形面积公式可建立关于t的方程,解方程求出t的值即可;
(3)延长QE交AC于点D,若PE⊥AB,则QD∥AB,所以可得△CQD∽△CBA,由相似三角形的性质:对应边的比值相等可求出DE=0.5t,易证△ABC∽△DPE,再由相似三角形的性质可得![]() ,把已知数据代入即可求出t的值.
,把已知数据代入即可求出t的值.
解:(1)当t=2时,
∵点P从A出发沿AC向C点以1厘米/秒的速度匀速移动;点Q从C出发沿CB向B点以2厘米/秒的速度匀速移动,
∴AP=2厘米,QC=4厘米,
∴PC=4,在Rt△PQC中PQ=![]() =
=![]() 厘米;
厘米;
(2)∵点P从A出发沿AC向C点以1厘米/秒的速度匀速移动;点Q从C出发沿CB向B点以2厘米/秒的速度匀速移动,
∴PC=AC﹣AP=6﹣t,CQ=2t,
∴S△CPQ=![]() CPCQ=
CPCQ=![]() ,
,
∴t2﹣6t+5=0
解得t1=1,t2=5(不合题意,舍去)
∴当t=1秒时,△PCQ的面积等于5cm2;
(3)能垂直,理由如下:
延长QE交AC于点D,
∵将△PQC翻折,得到△EPQ,
∴△QCP≌△QEP,
∴∠C=∠QEP=90°,
若PE⊥AB,则QD∥AB,
∴△CQD∽△CBA,
∴![]() ,
,
∴![]() ,
,
∴QD=2.5t,
∵QC=QE=2t
∴DE=0.5t
易证△ABC∽△DPE,
∴![]()
∴![]() ,
,
解得:t=![]() (0≤t≤4),
(0≤t≤4),
综上可知:当t=![]() 时,PE⊥AB.
时,PE⊥AB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(-3,2)关于y轴的对称点P′的坐标是( )
A. (-3,2) B. ( 3,-2)
C. ( 3,2) D. (-3,-2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】截止2016年4月28日,电影《美人鱼》的累计票房达到大约3390000000元,数据3390000000用科学记数法表示为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.
(1)如图1,若点O在BC上,求证:AB=AC;
(2)如图2,若点O在△ABC的内部,求证:AB=AC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】有四张正面分别标有数字2,1,﹣3,﹣4的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上,洗匀后从四张卡片中随机地摸取一张不放回,将该卡片上的数字记为m,再随机地摸取一张,将卡片上的数字记为n.
(1)请画出树状图并写出(m,n)所有可能的结果;
(2)求所选出的m,n能使一次函数y=mx+n的图象经过第二、三、四象限的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD的边AB上任取一点E,作EF⊥AB交BD于点F,取FD的中点G,连接EG、CG,如图(1),易证 EG=CG且EG⊥CG.
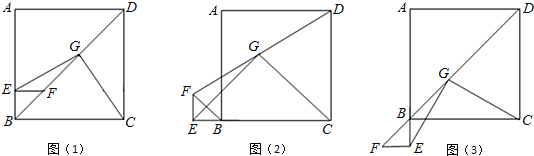
(1)将△BEF绕点B逆时针旋转90°,如图(2),则线段EG和CG有怎样的数量关系和位置关系?请直接写出你的猜想.
(2)将△BEF绕点B逆时针旋转180°,如图(3),则线段EG和CG又有怎样的数量关系和位置关系?请写出你的猜想,并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校组织了一次知识竞赛,共有25道题,每一道题答对得5分,答错或不答都扣3分,小明得了85分,那么他答对的题数是( )
A.22
B.20
C.19
D.18
相关试题

