【题目】在![]() 中,
中,![]() 于
于![]() ,
,![]() 是
是![]() 的平分线,
的平分线,![]() ,
,![]() ,求
,求![]() 和
和![]() 的度数.
的度数.

参考答案:
【答案】30°;20°;
【解析】
由CD⊥AB与∠B=60°,根据两锐角互余,即可求得∠BCD的度数;由∠A=20°,∠B=60°,求得∠ACB的度数,由CE是∠ACB的平分线,可求得∠ACE的度数,然后根据三角形外角的性质,求得∠CEB的度数,继而可得.
(1)∵CD⊥AB,
∴∠CDB=90°,
∵∠B=60°,
∴∠BCD=90°∠B=90°60°=30°;
∵∠A=20°,∠B=60°,∠A+∠B+∠ACB=180°,
∴∠ACB=100°,
∵CE是∠ACB的平分线,
∴∠ACE=![]() ∠ACB=50°,
∠ACB=50°,
∴∠CEB=∠A+∠ACE=20°+50°=70°,
∠ECD=90°70°=20°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车销售公司经销某品牌A款汽车,随着汽车的普及,其价格也在不断下降,今年5月份A款汽车的售价比去年同期每辆降价1万元,如果卖出相同数量的A款汽车,去年销售额为90万元,今年销售额只有80万元.
(1)今年5月份A款汽车每辆售价多少万元?
(2)为了增加收入,汽车销售公司决定再经销同品牌的B款汽车,已知B款汽车每辆进价为7.5万元,每辆售价为10.5万元,A款汽车每辆进价为6万元,若卖出这两款汽车15辆后获利不低于38万元,问B款汽车至少卖出多少辆?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列平面图形中,既是轴对称图形,又是中心对称图形的是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是⊙O外一动点,PA、PB、CD是⊙O的三条切线,C、D分别在PA、PB上,连接OC、OD.设∠P为x°,∠COD为y°,则y随x的函数关系图象为( )

A.
 B.
B. 
C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂计划生产
 两种产品共60件,需购买甲、乙两种材料.生产一件
两种产品共60件,需购买甲、乙两种材料.生产一件 产品需甲种材料4千克;生产一件
产品需甲种材料4千克;生产一件 产品需甲、乙两种材料各3千克.经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.
产品需甲、乙两种材料各3千克.经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂用于购买甲、乙两种材料的资金不超过9900元,且生产
 产品不少于38件,问符合生产条件的生产方案有哪几种?
产品不少于38件,问符合生产条件的生产方案有哪几种?(3)在(2)的条件下,若生产一件
 产品需加工费40元,生产一件
产品需加工费40元,生产一件 产品需加工费50元,应选择哪种生产方案,使生产这60件产品的成本最低(成本=材料费+加工费)?
产品需加工费50元,应选择哪种生产方案,使生产这60件产品的成本最低(成本=材料费+加工费)? -
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,任意一个正整数
 都可以进行这样的分解:
都可以进行这样的分解: (
( 是正整数,且
是正整数,且 ),在
),在 的所有这种分解中,如果
的所有这种分解中,如果 两因数之差的绝对值最小,我们就称
两因数之差的绝对值最小,我们就称 是
是 的最佳分解,产规定:
的最佳分解,产规定: ,例如:12可以分解成
,例如:12可以分解成 ,
, ,
, ,因为
,因为 ,所以
,所以 是12的最佳分解,所以
是12的最佳分解,所以 .
.(1)求
 ;
;(2)若正整数
 是4的倍数,我们称正整数
是4的倍数,我们称正整数 为“四季数”,如果一个两位正整数
为“四季数”,如果一个两位正整数 ,
, (
( ,
, 为自然数),交换个位上的数字与十位上的数字得到的新两位正整数减去原来的两位正整数所得的差为“四季数”,那么我们称这个数
为自然数),交换个位上的数字与十位上的数字得到的新两位正整数减去原来的两位正整数所得的差为“四季数”,那么我们称这个数 为“有缘数”,求所有“有缘数”中
为“有缘数”,求所有“有缘数”中 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中
 ,
, 且满足
且满足 ,长方形
,长方形 在坐标系中(如图),点
在坐标系中(如图),点 为坐标系的原点.
为坐标系的原点.
(1)求点
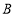 的坐标.
的坐标.(2)如图1,若点
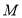 从点
从点 出发,以2个单位/秒的速度向右运动(不超过点
出发,以2个单位/秒的速度向右运动(不超过点 ),点
),点 从原点
从原点 出发,以1个单位/秒的速度向下运动(不超过点
出发,以1个单位/秒的速度向下运动(不超过点 ),设
),设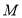 、
、 两点同时出发,在它们运动的过程中,四边形
两点同时出发,在它们运动的过程中,四边形 的面积是否发生变化?若不变,求其值;若变化,求变化的范围.
的面积是否发生变化?若不变,求其值;若变化,求变化的范围.(3)如图2,
 为
为 轴负半轴上一点,且
轴负半轴上一点,且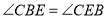 ,
,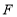 是
是 轴正半轴上一动点,
轴正半轴上一动点, 的平分线
的平分线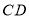 交
交 的延长线于点
的延长线于点 ,在点
,在点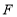 运动的过程中,请探究
运动的过程中,请探究 与
与 的数量关系,并说明理由.
的数量关系,并说明理由.
相关试题

