【题目】如图,四边形ABCD是正方形,E是AD上任意一点,延长BA到F,使得AF=AE,连接DF:
(1)旋转△ADF可得到哪个三角形?
(2)旋转中心是哪一点?旋转了多少度?
(3)BE与DF的数量关系、位置关系如何?为什么?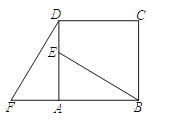
参考答案:
【答案】解:(1)旋转△ADF可得△ABE,
理由如下:
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=∠DAF=90°,
在△ADF和△ABE中,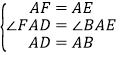 ,
,
∴△ADF≌△ABE,
∴旋转△ADF可得△ABE;
(2)由旋转的定义可知:旋转中心为A,因为AD=AB,所以AD和AB之间的夹角为旋转角即90°;
(3)BE=DF且BE⊥BE.理由如下:
延长BE交F于H点,如图,
∵四边形ABCD为正方形,
∴AD=AB,∠DAB=90°,
∵△ABE按逆时针方向旋转90°△ADF,
∴BE=DF,∠1=∠2,
∵∠3=∠4,
∴∠DHB=∠BAE=90°,
∴BE⊥DF.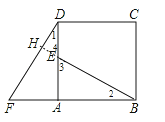
【解析】(1)旋转△ADF可得△ABE,通过证明△ADF≌△ABE即可说明问题;
(2)旋转的定义和旋转角的定义解答即可;
(3)根据旋转的性质得BE=DF,∠1=∠2,再根据三角形内角定理得到∠DHB=∠BAE=90°,所以BE⊥DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠AOB=70°,∠AOC=30°,OD平分∠BOC.请依题意补全图形,并求∠AOD的度数.
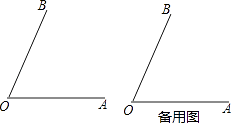
-
科目: 来源: 题型:
查看答案和解析>>【题目】要反映无锡一周内每天的最高气温的变化情况,宜采用______统计图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(-a5)4(-a2)3=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆汽车从A地驶往B地,前
 路段为普通公路,其余路段为高速公路,已知汽车在普通公路上行驶的速度为60km/h,在高速公路上行驶的速度为100km/h,汽车从A地到B地一共行驶了11h.请你根据以上信息,就该汽车行驶的“路程”或“时间”提出一个用二元一次方程组解决的问题,并写出解答过程.
路段为普通公路,其余路段为高速公路,已知汽车在普通公路上行驶的速度为60km/h,在高速公路上行驶的速度为100km/h,汽车从A地到B地一共行驶了11h.请你根据以上信息,就该汽车行驶的“路程”或“时间”提出一个用二元一次方程组解决的问题,并写出解答过程. -
科目: 来源: 题型:
查看答案和解析>>【题目】﹣5a(3a﹣2b)= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣2x(x﹣2)=________
相关试题

