【题目】对于实数![]() ,
,![]() 定义两种新运算“※”和“
定义两种新运算“※”和“![]() ”:
”: ![]() ※
※![]() ,
,![]() (其中
(其中![]() 为常数,且
为常数,且![]() ,若对于平面直角坐标系
,若对于平面直角坐标系![]() 中的点
中的点![]() ,有点
,有点![]() 的坐标
的坐标![]() ※
※![]() ,
,![]() 与之对应,则称点
与之对应,则称点![]() 的“
的“![]() 衍生点”为点
衍生点”为点![]() .例如:
.例如:![]() 的“2衍生点”为
的“2衍生点”为![]() ,即
,即![]() .
.
(1)点![]() 的“3衍生点”的坐标为 ;
的“3衍生点”的坐标为 ;
(2)若点![]() 的“5衍生点”
的“5衍生点” ![]() 的坐标为
的坐标为![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)若点![]() 的“
的“![]() 衍生点”为点
衍生点”为点![]() ,且直线
,且直线![]() 平行于
平行于![]() 轴,线段
轴,线段![]() 的长度为线段
的长度为线段![]() 长度的3倍,求
长度的3倍,求![]() 的值.
的值.
参考答案:
【答案】(1)![]() ;(2)点
;(2)点![]() ;(3)k=±3.
;(3)k=±3.
【解析】
(1)直接利用新定义进而分析得出答案;
(2)直接利用新定义结合二元一次方程组的解法得出答案;
(3)先由![]() 轴得出点
轴得出点![]() 的坐标为
的坐标为![]() ,继而得出点
,继而得出点![]() 的坐标为
的坐标为![]() ,由线段
,由线段![]() 的长度为线段
的长度为线段![]() 长度的3倍列出方程,解之可得.
长度的3倍列出方程,解之可得.
(1)点![]() 的“3衍生点”
的“3衍生点” ![]() 的坐标为
的坐标为![]() ,即
,即![]() ,
,
故答案为:![]() ;
;
(2)设![]()
依题意,得方程组![]() .
.
解得![]() .
.
![]() 点
点![]() ;
;
(3)设![]() ,则
,则![]() 的坐标为
的坐标为![]() .
.
![]() 平行于
平行于![]() 轴
轴
![]() ,即
,即![]() ,
,
又![]() ,
,
![]() .
.
![]() 点
点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
![]() 线段
线段![]() 的长度为
的长度为![]() .
.
![]() 线段
线段![]() 的长为
的长为![]() .
.
根据题意,有![]() ,
,
![]() .
.
∴k=±3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】①已知:△ABC中,BC=m,∠A=60°.问满足此条件的三角形有多少个?它们的最大面积存在吗?若存在求出最大面积,并回答此时三角形的形状;若不存在,请说明理由.

②有一个正方形的养鱼塘,四个角各有一棵大树.生产队设想把鱼塘扩大,使它成为一个面积最大的正方形,而又不把树挖掉,这一设想能否实现?若能,请你设计画出图形,并证明此时面积最大.若不能,请说明理由.

③上问题推广,有一个正五边形的养鱼塘,五个角各有一棵树,要扩大使它成为面积最大的正五边形,而又不把树挖掉,可以吗?画图说明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某文化用品商店用
 元采购一批书包,上市后发现供不应求,很快销售完了.商店又去采购第二批同样款式的书包,进货单价比第一次高
元采购一批书包,上市后发现供不应求,很快销售完了.商店又去采购第二批同样款式的书包,进货单价比第一次高 元,商店用了
元,商店用了 元,所购数量是第一次的
元,所购数量是第一次的 倍.
倍.(1)求第一批采购的书包的单价是多少元?
(2)若商店按售价为每个书包
 元,销售完这两批书包,总共获利多少元?
元,销售完这两批书包,总共获利多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】某校研究性学习小组在研究有关二次函数及其图象性质的问题时,发现了两个重要结论.一是发现抛物线y=ax2+2x+3(a≠0),当实数a变化时,它的顶点都在某条直线上;二是发现当实数a变化时,若把抛物线y=ax2+2x+3的顶点的横坐标减少
 ,纵坐标增加
,纵坐标增加 ,得到A点的坐标;若把顶点的横坐标增加
,得到A点的坐标;若把顶点的横坐标增加 ,纵坐标增加
,纵坐标增加 ,得到B点的坐标,则A、B两点一定仍在抛物线y=ax2+2x+3上.
,得到B点的坐标,则A、B两点一定仍在抛物线y=ax2+2x+3上.(1)请你协助探求出当实数a变化时,抛物线y=ax2+2x+3的顶点所在直线的解析式;
(2)问题(1)中的直线上有一个点不是该抛物线的顶点,你能找出它来吗?并说明理由;
(3)在他们第二个发现的启发下,运用“一般﹣一特殊﹣一般”的思想,你还能发现什么?你能用数学语言将你的猜想表述出来吗?你的猜想能成立吗?若能成立请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系内,
 的三个顶点坐标分别为
的三个顶点坐标分别为 (2,-4),
(2,-4),  (4,-4),
(4,-4),  (1,-1).
(1,-1).
(1)画出
 关于
关于 轴对称的
轴对称的 ,直接写出点
,直接写出点 的坐标;
的坐标;(2)画出
 绕点
绕点 逆时针旋转90°后的
逆时针旋转90°后的 ;
;(3)在(2)的条件下,求线段
 扫过的面积(结果保留π).
扫过的面积(结果保留π). -
科目: 来源: 题型:
查看答案和解析>>【题目】将不等式组
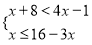 的解集在数轴上表示出来,正确的是( )
的解集在数轴上表示出来,正确的是( )A.
 B.
B. 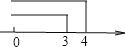
C.
 D.
D. 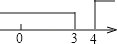
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的三边长分别为a,b,c.
(1)若a,b,c满足a2+b2+c2=ab+bc+ca,试判断△ABC的形状;
(2)若a=5,b=2,且c为整数,求△ABC的周长的最大值及最小值.
相关试题

