【题目】如图,在△ABC,AB=AC,DE⊥AB于点E,DF⊥AC于点F,BD=CD
求证:DE=DF

证明:∵AB=AC
∴∠B=∠C( ),
∵DE⊥AB,DF⊥AC
∴∠BED=∠DFC=90°
在△BDE和△CDF中

∴△BDE≌△CDF( ).
∴DE=DF( )
(1)请在括号里写出推理的依据.
(2)请你写出另一种证明此题的方法.
参考答案:
【答案】(1)等边对等角;AAS;全等三角形的对应边相等;(2)见解析
【解析】
(1)由AB=AC得∠B=∠C是依据“等边对等角”,由判定条件可知全等的依据是“AAS”,由全等得对应边相等是依据全等三角形的性质,据此作答即可;
(2)连接AD,根据等腰三角形三线合一的性质和角平分线的性质定理即可得证;
解:(1)证明:∵AB=AC
∴∠B=∠C(等边对等角),
∵DE⊥AB,DF⊥AC
∴∠BED=∠DFC=90°
在△BDE和△CDF中

∴△BDE≌△CDF(AAS).
∴DE=DF(全等三角形的对应边相等)
故答案为等边对等角;AAS;全等三角形的对应边相等.
(2)连接AD.

∵AB=AC,BD=CD,
∴AD平分∠BAC,
又∵DE⊥AB,DF⊥AC,
∴DE=DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠ABC=∠ACB,把这个三角形折叠,使得点B与点A重合,折痕分别交直线AB,AC于点M,N,若∠ANM=50°,则∠B的度数为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
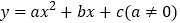 的图象如图所示,有下列
的图象如图所示,有下列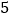 个结论:
个结论:①
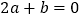 ;②
;②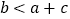 ;③
;③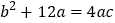 ;④
;④ ,(
,(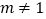 的实数);⑤
的实数);⑤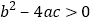 ,其中正确的结论有________.
,其中正确的结论有________.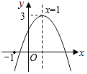
-
科目: 来源: 题型:
查看答案和解析>>【题目】把大小和形状完全相同的
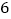 张卡片分成两组,每组
张卡片分成两组,每组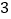 张,分别标上
张,分别标上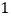 、
、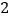 、
、 ,将这两组卡片分别放入两个盒子中搅匀,再从中随机抽取一张.
,将这两组卡片分别放入两个盒子中搅匀,再从中随机抽取一张. 请用画树状图的方法求取出的两张卡片数字之和为奇数的概率;
请用画树状图的方法求取出的两张卡片数字之和为奇数的概率; 若取出的两张卡片数字之和为奇数,则甲胜;取出的两张卡片数字之和为偶数,则乙胜;试分析这个游戏是否公平?请说明理由.
若取出的两张卡片数字之和为奇数,则甲胜;取出的两张卡片数字之和为偶数,则乙胜;试分析这个游戏是否公平?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,二次函数
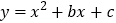 的图象与
的图象与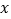 轴交于
轴交于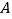 、
、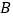 两点,
两点,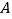 点在原点的左则,
点在原点的左则,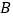 点的坐标为
点的坐标为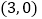 ,与
,与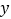 轴交于
轴交于 点,点
点,点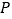 是直线
是直线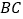 下方的抛物线上一动点.
下方的抛物线上一动点.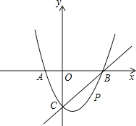
 求这个二次函数的表达式;
求这个二次函数的表达式; 求出四边形
求出四边形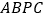 的面积最大时的
的面积最大时的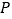 点坐标和四边形
点坐标和四边形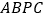 的最大面积;
的最大面积;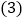 连结
连结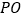 、
、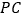 ,在同一平面内把
,在同一平面内把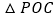 沿
沿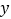 轴翻折,得到四边形
轴翻折,得到四边形 ,是否存在点
,是否存在点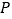 ,使四边形
,使四边形 为菱形?若存在,请求出此时点
为菱形?若存在,请求出此时点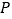 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由; 在直线
在直线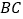 找一点
找一点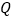 ,使得
,使得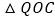 为等腰三角形,请直接写出
为等腰三角形,请直接写出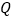 点坐标.
点坐标. -
科目: 来源: 题型:
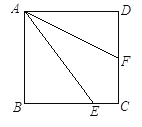
查看答案和解析>>【题目】如图,正方形ABCD中,E为BC上一点,AF平分∠DAE,求证:BE+DF=AE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
 ,已知抛物线
,已知抛物线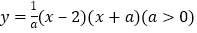 与
与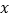 轴从左至右交于
轴从左至右交于 ,
,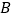 两点,与
两点,与 轴交于点
轴交于点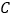 .
.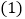 若抛物线过点
若抛物线过点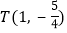 ,求抛物线的解析式;
,求抛物线的解析式;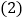 在第二象限内的抛物线上是否存在点
在第二象限内的抛物线上是否存在点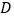 ,使得以
,使得以 、
、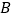 、
、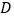 三点为顶点的三角形与
三点为顶点的三角形与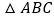 相似?若存在,求
相似?若存在,求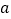 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.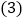 如图
如图 ,在
,在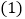 的条件下,点
的条件下,点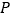 的坐标为
的坐标为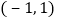 ,点
,点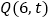 是抛物线上的点,在
是抛物线上的点,在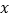 轴上,从左至右有
轴上,从左至右有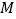 、
、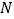 两点,且
两点,且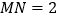 ,问
,问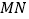 在
在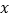 轴上移动到何处时,四边形
轴上移动到何处时,四边形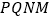 的周长最小?请直接写出符合条件的点
的周长最小?请直接写出符合条件的点 的坐标.
的坐标.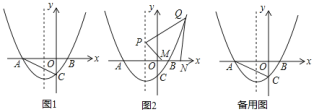
相关试题

