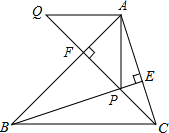
【题目】如图,BE、CF是△ABC的高且相交于点P,AQ∥BC交CF延长线于点Q,若有BP=AC,CQ=AB,线段AP与AQ的关系如何?说明理由。
参考答案:
【答案】证明见解析
【解析】试题分析:
由BE、CF是△ABC的高,易得∠ABP+∠BPF=90°,∠ACP+∠CPE=90°,结合∠BPF=∠CPE,易得∠ABP=∠ACP,这样结合BP=AC,CQ=AB,即可由“SAS”证得△ACQ≌△PBA,从而可得AP=AQ,∠Q=∠PAF,结合∠PAF+∠APF=90°,可得:∠APF+∠Q=90°,即可得到∠QAP=90°,从而可得AQ⊥AP,由此即可得到AQ与AP的关系是相等且互相垂直.
试题解析:
AQ与AP的关系是:相等且互相垂直,理由如下:
∵BE、CF是△ABC的高,
∴∠BFP=∠CEP=90°,
∴∠ABP+∠BPF=90°,∠ACP+∠CPE=90°,
又∵∠BPF=∠CPE,
∴∠ABP=∠ACP,
在△ACQ和△PBA中:
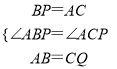 ,
,
∴△ACQ≌△PBA(SAS),
∴AP=AQ,∠Q=∠PAF,
∵∠PAF+∠APF=90°,
∴∠APF+∠Q=90°,
∴AP⊥AQ,即:AQ与AP的关系是相等且互相垂直.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有________和一条________对应相等的两个直角三角形全等,简写成“斜边直角边”或用字母表示为“___________”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列条件能保证△ABC≌△ADC的是:①AB=AD,BC=DC;②∠1=∠3,∠4=∠2;③∠1=∠2,∠4=∠3;④∠1=∠2,AB=AD;⑤∠1=∠2,BC=DC.( )
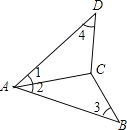
A. ①②③④⑤ B. ①②③④ C. ①③④ D. ①③④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】判定两个直角三角形全等的方法有______________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AC平分∠DAB,∠ACB=90°,E为AB的中点,连接CE、DE.AC与DE相交于点F.
(1)求证:△ADF∽△CEF;
(2) 若AD=4,AB=6,求
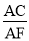 的值.
的值.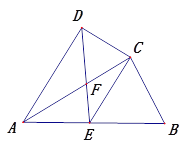
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:ma2﹣mb2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】大连外语学院98000人极其喜欢数学,此数表示为科学记数法( )
A.0.98×105B.9.8×104C.98×l03D.9.8×l03
相关试题

