【题目】如图所示,在矩形ABCD中,对角线AC,BD相交于点O,E是CD的中点,连接OE,过点C作CF∥BD交线段OE的延长线于点F,连接DF.求证: 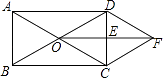
(1)OD=CF;
(2)四边形ODFC是菱形.
参考答案:
【答案】
(1)证明:∵CF∥BD,
∴∠DOE=∠CFE,
∵E是CD的中点,
∴CE=DE
在△ODE和△FCE中,
 ,
,
∴△ODE≌△FCE(ASA)
∴OD=CF.
(2)证明:由(1)知OD=CF,
∵CF∥BD,
∴四边形ODFC是平行四边形
在矩形ABCD中,OC=OD,
∴四边形ODFC是菱形.
【解析】(1)欲证明OD=CF,只要证明△ODE≌△FCE(ASA)即可.(2)首先证明四边形ODFC是平行四边形,再由OD=OC即可推出四边形ODFC是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,矩形ABCD的对角线相交于点O,OF⊥AD于点F,OF=2cm,AE⊥BD于点E,且BE﹕BD=1﹕4,求AC的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的三边长分别为a、b、4,且a、b是关于x的一元二次方程x2﹣12x+m+2=0的两根,求m的值.
-
科目: 来源: 题型:
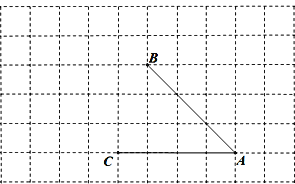
查看答案和解析>>【题目】如图,由相同边长的小正方形组成的网格图形,A、B、C都在格点上,利用网格画图:(注:所画线条用黑色签字笔描黑)
(1)过点C画AB的平行线;
(2)过点B画AC的垂线,垂足为点G;过点B画AB的垂线,交AC的延长线于H.
(3)点B到AC的距离是线段 的长度,线段AB的长度是点 到直线
的距离.
(4)线段BG、AB的大小关系为:BG AB(填“>”、“<”或“=”),理由是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了知道一张课桌所占的空间,应该通过测量收集数据,包括课桌的 、 和
-
科目: 来源: 题型:
查看答案和解析>>【题目】问卷调查有下列步骤,请按顺序排列为 (填序号).
①发下问卷让被调查人填写;②设计问卷;③对问卷的数据收集整理;④收起问卷. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AC为对角线,点E、F分别是边BC、AD的中点.
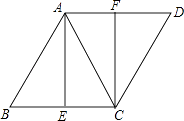
(1)求证:△ABE≌△CDF;
(2)若∠B=60°,AB=4,求线段AE的长.
相关试题

