【题目】如图，正方形网格中的每个小正方形的边长都是1，每个小格的顶点叫做格点．
（1）在图1中以格点为顶点画一个面积为5的正方形；

（2）在图2中以格点为顶点画一个三角形，使三角形三边长分别为2、 、 ；

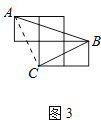
（3）如图3，A、B、C是小正方形的顶点，求∠ABC．

参考答案：

【答案】
（1）解：如图所示：


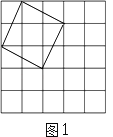
（2）解：如图所示：


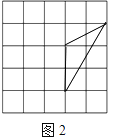
（3）解：连接AC，

由勾股定理得：AC=BC= ，AB= ，

∵AC2+BC2=AB2=10，

∴△ABC为等腰直角三角形

∴∠ABC=45°


【解析】（1）面积为5的正方形的边长为 ，画出正方形即可；（2）以直角边为1和2构造斜边为 ，再以2和3为直角边构造斜边为 就得到三角形三边长分别为2、 、 ；（3）连接AC，利用勾股定理的逆定理证明△ACB为直角三角形即可得到∠ABC的度数．

关闭