搜索
【题目】解方程
（1）﹣2x=4
（2）x﹣10=7
（3）x+13=5x+37
（4）3x﹣x=﹣ 
+1．
参考答案：
【答案】
（1）解：-2x=4，
解得：x=﹣2
（2）解：x﹣10=7，
解得：x=17
（3）解：x+13=5x+37，
移项合并得：4x=﹣24，
解得：x=﹣6
（4）解：3x﹣x=﹣ 
+1，
合并得：2x= ，
解得：x= 
【解析】（1）方程x系数化为1，即可求出解；（2）方程移项合并，即可求出解；（3）方程移项合并，把x系数化为1，即可求出解；（4）方程合并后，将x系数化为1，即可求出解．
【考点精析】根据题目的已知条件，利用解一元一次方程的步骤的相关知识可以得到问题的答案，需要掌握先去分母再括号，移项变号要记牢．同类各项去合并，系数化“1”还没好．求得未知须检验，回代值等才算了．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若多项式x2＋px＋8与x2－3x＋q的积中不含x2项，也不含x3项，求p和q的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】先化简，再求值
（1）4x﹣x2+2x3﹣（3x2+x+2x3），其中x=3．
（2）4x2﹣xy﹣（
y2+2x2）+2（3xy﹣ 
y2），其中x=5，y= 
． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知，△ABC是边长3cm的等边三角形．动点P以1cm/s的速度从点A出发，沿线段AB向点B运动．
（1）如图1，设点P的运动时间为t（s），那么t为何值时，△PBC是直角三角形；
（2）若另一动点Q从点C出发，沿射线BC方向运动．连接PQ交AC于D．如果动点P，Q都以1cm/s的速度同时出发．
①如图2，设运动时间为t（s），那么t为何值时，△DCQ是等腰三角形？
②如图3，连接PC，请你猜想：在点P，Q的运动过程中，△PCD和△QCD的面积有什么关系？并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某公司组织部分员工到一博览会的A、B、C、D、E五个展馆参观，公司所购门票种类、数量绘制成的条形和扇形统计图如图所示． 请根据统计图回答下列问题：
（1）将条形统计图和扇形统计图在图中补充完整；
（2）若
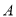馆门票仅剩下一张，而员工小明和小华都想要，他们决定采用抽扑克牌的方法来确定，规则是：“将同一副牌中正面分别标有数字1，2，3，4的四张牌洗匀后，背面朝上放置在桌面上，每人随机抽一次且一次只抽一张；一人抽后记下数字，不放回再由另一人抽．若小明抽得的数字比小华抽得的数字大，门票给小明，否则给小华．” 请用画树状图或列表的方法计算出小明和小华获得门票的概率，并说明这个规则对双方是否公平．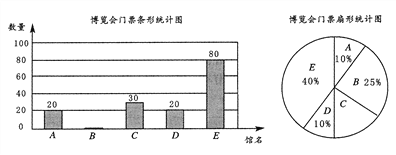
-
科目： 来源： 题型：
查看答案和解析>>【题目】解答
（1）如图（1），已知：在△ABC中，∠BAC=90°，AB=AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D，E．
证明：DE=BD+CE．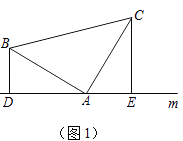
（2）如图（2），将（1）中的条件改为：在△ABC中，AB=AC，D，A，E三点都在直线m上，并且有∠BDA=∠AEC=∠BAC=α，其中α为任意锐角或钝角．请问结论DE=BD+CE是否成立？如成立，请你给出证明；若不成立，请说明理由．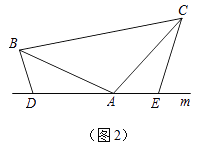
（3）拓展与应用：如图（3），D，E是D，A，E三点所在直线m上的两动点（D，A， E三点互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD，CE，若∠BDA=∠AEC=∠BAC，试判断△DEF的形状．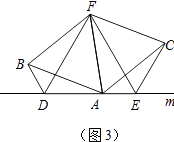
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，∠C = 90°,AD是∠BAC的平分线，DE⊥AB于E，若DE = 8cm，DB = 10cm则BC等于( )
A.14cm
B.16cm
C.18cm
D.20cm
相关试题
