【题目】在平面直角坐标系xOy中,抛物线![]() 与x轴交于A,B两点(点A在点B的左侧).
与x轴交于A,B两点(点A在点B的左侧).
(1)求点A,B的坐标及抛物线的对称轴;
(2)过点B的直线l与y轴交于点C,且![]() ,直接写出直线l的表达式;
,直接写出直线l的表达式;
(3)如果点![]() 和点
和点![]() 在函数
在函数![]() 的图象上,PQ=2a且
的图象上,PQ=2a且![]() , 求
, 求![]() 的值.
的值.
参考答案:
【答案】(1)A点坐标为(0,0),B点坐标为(4,0).对称轴为直线: ![]() .(2)
.(2)![]() ,
, ![]() .(3)6.
.(3)6.
【解析】(1)首先解一元二次方程求出A、B点坐标,然后利用抛物线的对称轴公式求得;(2)利用已知条件直接写出直线l的表达式即可;(3)由二次函数的性质得出点P与点Q关于对称轴直线,把x1、x2的值代入原式即可.
解:(1)把y=0代入![]() 得
得![]() ,
,
因式分解得: ![]() ,
,
∴![]() ,
,
∵点A在点B的左侧
∴A点坐标为(0,0),B点坐标为(4,0).
对称轴为直线: ![]() .
.
(2)![]() ,
, ![]() .
.
(3)∵点![]() 和点
和点![]() 在函数
在函数![]() 的图象上,
的图象上,
∴点P与点Q关于对称轴直线![]() 对称.
对称.
∵![]() ,
, ![]()
∴![]() 和
和![]() .
.
代入![]() 得:原式=6.
得:原式=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请说出以下几个点在坐标轴的哪部分上.(2, 0)、(0, 4)、(1, 0)、(0,3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中,结果最小的是( )
A. 2+(-3) B. 2×(-3) C. 2-(-3) D. -32
-
科目: 来源: 题型:
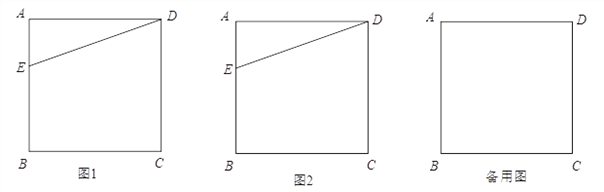
查看答案和解析>>【题目】如图,在正方形ABCD中,E为AB边上一点,连接DE,将△ADE绕点D逆时针旋转90°得到△CDF,作点F关于CD的对称点,记为点G,连接DG.
(1)依题意在图1中补全图形;
(2)连接BD,EG,判断BD与EG的位置关系并在图2中加以证明;
(3)当点E为线段AB的中点时,直接写出∠EDG的正切值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(﹣2,y1)、B(1,y2)在二次函数y=x2+2x+2的图象上,y1与y2的大小关系为( )
A.y1>y2B.y1=y2C.y1<y2D.y1≤y2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
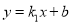 与x轴、y轴相交于P、Q两点,与y=
与x轴、y轴相交于P、Q两点,与y=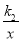 的图像相交于A(-2,m)、B(1,n)两点,连接OA、OB. 给出下列结论: ①k1k2<0;②m+
的图像相交于A(-2,m)、B(1,n)两点,连接OA、OB. 给出下列结论: ①k1k2<0;②m+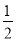 n=0; ③S△AOP= S△BOQ;④不等式k1x+b>
n=0; ③S△AOP= S△BOQ;④不等式k1x+b>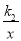 的解集是x<-2或0<x<1,其中正确的结论是 ( )
的解集是x<-2或0<x<1,其中正确的结论是 ( ) 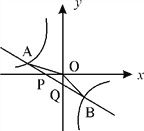
A. ②③④ B. ①②③④ C. ③④ D. ②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】将二次函数y=x2﹣4x+7化为y=(x﹣h)2+k的形式,结果为y=_____.
相关试题

