【题目】如图1,将半径为2的圆形纸片沿圆的两条互相垂直的直径AC,BD两次折叠后,得到如图2所示的扇形OAB,然后再沿OB的中垂线EF将扇形OAB剪成左右两部分,则∠OEF=°;右边部分经过两次展开并压平后所得的图形的周长为 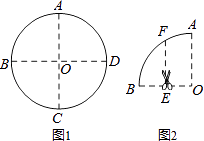
参考答案:
【答案】90;![]() +4
+4 ![]()
【解析】解:如图3, 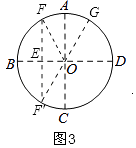
∵EF是OB的中垂线,
∴∠OEF=90°,OE= ![]() OB=
OB= ![]() OF,
OF,
∴∠EFO=30°,∠EOF=60°,
由勾股定理得:EF= ![]() =
= ![]() ,
,
由折叠得:∠F′OF=120°,
∴∠FOA=30°,
∴∠FOG=60°,
则右边部分经过两次展开并压平后所得的图形的周长为:
2 ![]() +2F′F=
+2F′F= ![]() ×2+2×2
×2+2×2 ![]() =
= ![]() +4
+4 ![]() .
.
故答案为:90, ![]() +4
+4 ![]() .
.
根据沿OB的中垂线EF将扇形OAB剪成左右两部分,可知∠OEF=90°,所以E是OB的中点,则OE= ![]() OB=
OB= ![]() OF,则∠EFO=30°,得出
OF,则∠EFO=30°,得出 ![]() 所对的圆周角∠FOG=60°,根据勾股定理求出直角边FE=
所对的圆周角∠FOG=60°,根据勾股定理求出直角边FE= ![]() ,所以FF′=2
,所以FF′=2 ![]() ,从而得出结论.
,从而得出结论.
-
科目: 来源: 题型:
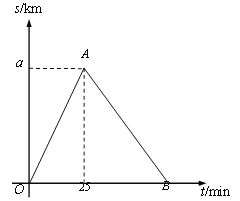
查看答案和解析>>【题目】某市举行“迷你马拉松”长跑比赛,运动员从起点甲地出发,跑到乙地后,沿原路线再跑回点甲地.设该运动员离开起点甲地的路程s(km)与跑步时间t(min)之间的函数关系如图所示.已知该运动员从甲地跑到乙地时的平均速度是0.2 km/min,根据图像提供的信息,解答下列问题:
(1)a= km;
(2)组委会在距离起点甲地3km处设立一个拍摄点P,该运动员从第一次过P点到第二次过P点所用的时间为24min.
①求AB所在直线的函数表达式;
②该运动员跑完全程用时多少min?
-
科目: 来源: 题型:
查看答案和解析>>【题目】纳米是一种长度单位,1米=109纳米,已知某种植物花粉的直径约为35000纳米,那么用科学记数法表示这种花粉的直径为( )
A. 3.5×10﹣6米B. 3.5×10﹣5米C. 35×1013米D. 3.5×1013米
-
科目: 来源: 题型:
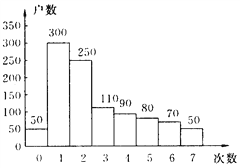
查看答案和解析>>【题目】某小区便民超市为了了解顾客的消费情况,在该小区居民中进行调查,询问每户人家每周到超市的次数,下图是根据调查结果绘制的,请问:
(1)这种统计图通常被称为什么统计图?(2)此次调查共询问了多少户人家?
(3)超过半数的居民每周去多少次超市?(4)请将这幅图改为扇形统计图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①、②、③是三个可以自由转动的转盘.
(1)若同时转动①、②两个转盘,则两个转盘停下时指针所指的数字都是2的概率为 ;
(2)甲、乙两人用三个转盘玩游戏,甲转动转盘,乙记录指针停下时所指的数字.游戏规定:当指针所指的三个数字中有数字相同时,就算甲赢,否则就算乙赢.请判断这个游戏是否公平,并说明你的理由.
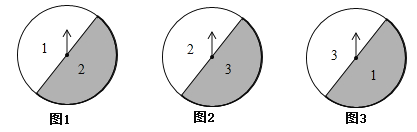
-
科目: 来源: 题型:
查看答案和解析>>【题目】人民商场销售某种冰箱,每台进价为2500元,市场调研表明:当每台销售价定为2900元时,平均每天能售出8台;每台售价每降低50元,平均每天能多售出4台.设该种冰箱每台的销售价降低了x元.
(1)填表:
每天售出的冰箱台数(台)
每台冰箱的利润(元)
降价前
8
降价后
(2)若商场要想使这种冰箱的销售利润平均每天达到5000元,则每台冰箱的售价应定为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某年级组织学生参加夏令营,分为甲、乙、丙三组进行活动.下面两幅统计图反映了学生报名参加夏令营的情况.请你根据图中的信息回答下列问题:
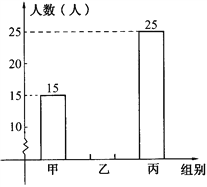
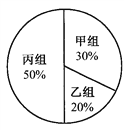
报名人数分布直方图 报名人数扇形统计图
(1)求该年级报名参加本次活动的总人数;
(2)求该年级报名参加乙组的人数,并补全频数分布直方图;
(3)根据实际情况,需从甲组抽调部分同学到丙组,使丙组人数是甲组人数的3倍,那么,应从甲组抽调多少名学生到丙组?
相关试题

