【题目】如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证:
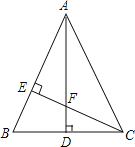
(1)△AEF≌△CEB;
(2)AF=2CD.
参考答案:
【答案】见解析
【解析】
试题分析:(1)由AD⊥BC,CE⊥AB,易得∠AFE=∠B,利用全等三角形的判定得△AEF≌△CEB;
(2)由全等三角形的性质得AF=BC,由等腰三角形的性质“三线合一”得BC=2CD,等量代换得出结论.
证明:(1)∵AD⊥BC,CE⊥AB,
∴∠BCE+∠CFD=90°,∠BCE+∠B=90°,
∴∠CFD=∠B,
∵∠CFD=∠AFE,
∴∠AFE=∠B
在△AEF与△CEB中,
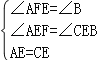 ,
,
∴△AEF≌△CEB(AAS);
(2)∵AB=AC,AD⊥BC,
∴BC=2CD,
∵△AEF≌△CEB,
∴AF=BC,
∴AF=2CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列轴对称图形中,对称轴最多的是( )
A. 等腰直角三角形 B. 圆 C. 正方形 D. 正三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下列已知条件,能惟一画出△ABC的是( )
A. AB=3,BC=4,CA=8 B. ∠A=60°,∠B=45°,AB=4
C. AB=4,BC=3,∠A=30° D. ∠C=90°,AB=6
-
科目: 来源: 题型:
查看答案和解析>>【题目】设

(1)请用含n的代数式表示
 (n为自然数);
(n为自然数);(2)探究
 是否为4的倍数,证明你的结论并用文字描述该结论;
是否为4的倍数,证明你的结论并用文字描述该结论;(3)若一个数的算术平方根是一个自然数,则称这个数是“完全平方数”(如:1,16等),试写出
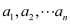 这些数中,前4个“完全平方数”。
这些数中,前4个“完全平方数”。 -
科目: 来源: 题型:
查看答案和解析>>【题目】李大叔想用篱笆围成一个周长为80米的矩形场地,矩形面积S(单位:平方米)随矩形一边长x(单位:米)的变化而变化.
(1)求S与x之间的函数关系式,并写出自变量x的取值范围;
(2)当x是多少时,矩形场地面积S最大?最大面积是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm.点P从A出发,沿AB方向,以2cm/s的速度向点B运动,点Q从C出发,沿CA方向,以1cm/s的速度向点A运动;若两点同时出发,当其中一点到达端点时,两点同时停止运动,设运动时间为t(s),△APQ的面积为S(cm2)
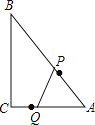
(1)t=2时,则点P到AC的距离是 cm,S= cm2;
(2)t为何值时,PQ⊥AB;
(3)t为何值时,△APQ是以AQ为底边的等腰三角形;
(4)求S与t之间的函数关系式,并求出S的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
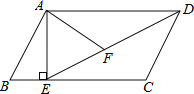
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6
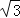 ,AF=4
,AF=4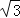 ,求AE的长.
,求AE的长.
相关试题

