Question

【题目】抛物线m：y=x2﹣2x+2与直线l：y=x+2交于A，B（A在B的左侧），且抛物线顶点为C．

（1）求A，B，C坐标；

（2）若点D为该抛物线上的一个动点，且在直线AC下方，当以A，C，D为顶点的三角形面积最大时，求点D的坐标及此时三角形的面积．

（3）将抛物线m：y=x2﹣2x+2沿直线OC方向平移得抛物线m′，与直线l：y=x+2交于A′，B′，问在平移过程中线段A′B′的长度是否发生变化，请通过计算说明．

Answer 1

【答案】（1）A（0，2），B（3，5），C（1，1）；（2）D（， ）；（3）A′B′的长度为定值，理由见解析

【解析】试题分析：（1）利用配方法得到y=（x﹣1）2+1，从而可得到点C的坐标，然后将y=x2﹣2x+2与y=x+2可求得点A和点B的坐标；

（2）过点D作DE∥y轴，交抛物线与点P．先求得直线AC的解析式，设点D的坐标为（m，m2﹣2m+2），则点P的坐标为（m，﹣m+2），则PD=﹣m2+m，然后依据S△ACD=S△APD+S△CPD的到△ACD的面积与m的函数关系式，最后，利用配方法可求解即可．

（3）过点A′作A′M⊥x轴，垂足为M，B′N⊥x轴，垂足为N，作A′G⊥B′N，垂足为G，则A′B′=A′G，设平移后抛物线的解析式为y=（x﹣a）2+a．A′（x1，y1）B′（x2，y2），依据完全平方公式得到A′G=．由将y=x+2代入y=（x﹣a）2+a得到关于x的方程，依据一元二次方程根与系数的关系可得到x2+x1=2a+1，x2x1=a2+a+2，从而可求得A′G的长，最后可得到A′B′的长．

试题解析：（1）∵y=x2﹣2x+2=（x﹣1）2+1，

∴C（1，1），

将y=x2﹣2x+2与y=x+2联立得： ，解得： 或，

∴A（0，2），B（3，5）；

（2）如图1所示：过点D作DE∥y轴，交抛物线与点P．

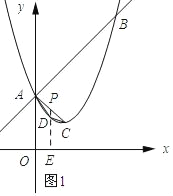
设AC的解析式为y=kx+b，将点A和点C的坐标代入得： ，解得k=﹣1，b=2，

∴直线AC的解析式为y=﹣x+2，

设点D的坐标为（m，m2﹣2m+2），则点P的坐标为（m，﹣m+2），则PD=（﹣m+2）﹣（m2﹣2m+2）=﹣m2+m．

S△ACD=S△APD+S△CPD=×1DP=（﹣m2+m）=﹣（m﹣）2+，

∴当m=时，△ACD的面积有最大值，最大值为，

此点D的坐标为（， ）；

（3）如图2所示：过点A′作A′M⊥x轴，垂足为M，B′N⊥x轴，垂足为N，作A′G⊥B′N，垂足为G，则A′B′=A′G，

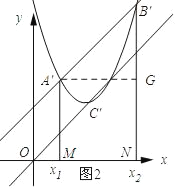
设OC的解析式为y=kx，将点C的坐标代入得到k=1，则OC的解析式为y=x，

设平移后抛物线的解析式为y=（x﹣a）2+a，

设A′（x1，y1）B′（x2，y2），则A′G=|x2﹣x1|= ，

将y=x+2代入y=（x﹣a）2+a得：x2﹣（2a+1）x+a2+a+2=0，

∴x2+x1=2a+1，x2x1=a2+a+2．

∴A′G= =3，

∴A′B′=3 ，

∴A′B′的长度为定值．