【题目】如图,在□ABCD中,点E,F分别是边AB,CD的中点,(1)求证:△CFB≌△AED;
(2)若∠ADB=90°,判断四边形BFDE的形状,并说明理由;

参考答案:
【答案】(1)见解析;(2) 四边形BFDE是菱形.
【解析】分析:(1)首先根据平行四边形的性质,得到相等的边角和平行线,然后根据中点的性质和全等三角形的判定SAS证明即可;
(2)连接EF,根据一组对边平行且相等的四边形是平行四边形证得:四边形四边形![]() 是平行四边形,四边形
是平行四边形,四边形![]() 是平行四边形,然后根据平行线的性质证明,最后得到对角线互相垂直的平行四边形是菱形.
是平行四边形,然后根据平行线的性质证明,最后得到对角线互相垂直的平行四边形是菱形.
详解:(1)证明:![]() 四边形
四边形![]() 是平行四边形
是平行四边形
∴![]() ,
,![]() ,
,![]()
又∵点E,F分别是AB,CD的中点
∴![]()
∴![]()
(2)解法一:四边形![]() 是菱形。证明如下:
是菱形。证明如下:
连接EF
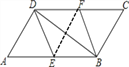
∵四边形![]() 是平行四边形
是平行四边形
∴![]()
又∵点E,F分别是AB,CD的中点
∴![]()
∴四边形![]() 是平行四边形
是平行四边形
同理,四边形![]() 是平行四边形
是平行四边形
∴![]()
∴![]()
∴![]()
∴四边形![]() 是菱形。
是菱形。
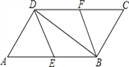
(2)解法二:四边形![]() 是菱形。证明如下:
是菱形。证明如下:
∵四边形![]() 是平行四边形
是平行四边形
∴![]()
又∵点E,F分别是AB,CD的中点
∴![]() ,
,![]()
∴四边形![]() 是平行四边形
是平行四边形
又∵![]()
∴在![]() 中,
中,![]()
∴四边形![]() 是菱形。
是菱形。
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题:
(1)25.7+(﹣7.3)+(﹣13.7)+7.3
(2)

(3)﹣14﹣(1﹣0.5)×

(4)

-
科目: 来源: 题型:
查看答案和解析>>【题目】【问题情境】
在△ABC中,AB=AC,点P为BC所在直线上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D、E,过点C作CF⊥AB,垂足为F.当P在BC边上时(如图1),求证:PD+PE=CF.

图① 图② 图③
证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.(不要证明)
【变式探究】
当点P在CB延长线上时,其余条件不变(如图3).试探索PD、PE、CF之间的数量关系并说明理由.
请运用上述解答中所积累的经验和方法完成下列两题:
【结论运用】
如图4,将长方形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE、PH⊥BC,垂足分别为G、H,若AD=8,CF=3,求PG+PH的值;
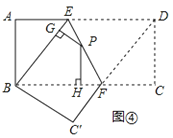
【迁移拓展】
在直角坐标系中.直线l1:y=
 与直线l2:y=2x+4相交于点A,直线l1、l2与x轴分别交于点B、点C.点P是直线l2上一个动点,若点P到直线l1的距离为1.求点P的坐标.
与直线l2:y=2x+4相交于点A,直线l1、l2与x轴分别交于点B、点C.点P是直线l2上一个动点,若点P到直线l1的距离为1.求点P的坐标.
-
科目: 来源: 题型:
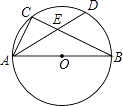
查看答案和解析>>【题目】如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=6,AD=5,则AE的长为( )
A.2.5
B.2.8
C.3
D.3.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城市街道上行驶速度不得超过70 km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方30 m处,过了2 s后,测得小汽车与车速检测仪间距离为50 m,这辆小汽车超速了吗?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知A点从(1,0)点出发,以每秒1个单位长的速度沿着x轴的正方向运动,经过t秒后,以O、A为顶点作菱形OABC,使B、C点都在第一象限内,且∠AOC=60°,又以P(0,4)为圆心,PC为半径的圆恰好与OA所在的直线相切,则t= .

-
科目: 来源: 题型:
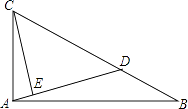
查看答案和解析>>【题目】如图,已知点D是Rt△ABC的斜边BC上的一点,tanB=
 ,BC=3BD,CE⊥AD,则
,BC=3BD,CE⊥AD,则 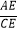 = .
= . 
相关试题

