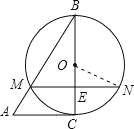
【题目】如图,在△ABC中,以BC为直径的⊙O交AB于M,弦MN∥AC且MN交BC于点E,ME=1,BM=2,BE=![]() .
.

(1)求证AC是⊙O的切线;
(2)求弧NC的长度.
参考答案:
【答案】(1)证明见解析(2)![]()
【解析】
试题分析:(1)根据勾股定理的逆定理证明∠BEM=90°,根据平行线的性质得到∠ACB=90°,根据切线的判定定理证明;
(2)根据正弦的定义和垂径定理求出∠CON=60°,利用弧长公式计算即可.
试题解析:(1)∵ME=1,BM=2,BE=![]() ,
,
∴ME2+BE2=1+3=4,BM2=4,
∴ME2+BE2=BM2,
∴∠BEM=90°,又MN∥AC,
∴∠ACB=∠BEM=90°,
∴AC是⊙O的切线;
(2)连接ON,
∵∠BEM=90°,ME=1,BM=2,
∴∠B=30°,![]() ,NE=ME=1,
,NE=ME=1,
∴∠CON=60°,
ON=![]() ,
,
故弧NC的长度为: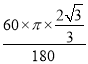 =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2﹣5ax+2(a≠0)与y轴交于点C,与x轴交于点A(1,0)和点B.

(1)求抛物线的解析式;
(2)求直线BC的解析式;
(3)若点N是抛物线上的动点,且点N在第四象限内,过点N作NH⊥x轴,垂足为H,以B,N,H为顶点的三角形是否能够与△OBC相似?若能,请求出所有符合条件点N的坐标;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,点P(4,5)关于y轴的对称点的坐标为( )
A. (﹣4,5)B. (4,﹣5)C. (4,5)D. (4,﹣3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列句子中,属于命题的有( )
A. 互为补角的两个角和为 90° B. 延长线段 AB
C. 画出长度为 π 的线段 D. 已知 a2=4 ,求 a 的值
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2-2(3x-2)+(x+1)=0的一般形式是( )
A.x2-5x+5=0 B.x2+5x-5=0 C.x2+5x+5=0 D.x2+5=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】写出两个一元二次方程,使每个方程都有一个根为0,并且二次项系数都为1: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线与x轴交于A(﹣1,0)、E(3,0)两点,与y轴交于点B(0,3).
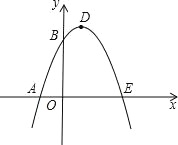
(1)求抛物线的解析式;
(2)设抛物线顶点为D,求四边形AEDB的面积;
(3)△AOB与△DBE是否相似?如果相似,请给以证明;如果不相似,请说明理由.
相关试题

