Question

【题目】如图，已知抛物线与x轴交于A（﹣1，0）、E（3，0）两点，与y轴交于点B（0，3）．

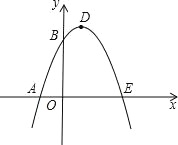
（1）求抛物线的解析式；

（2）设抛物线顶点为D，求四边形AEDB的面积；

（3）△AOB与△DBE是否相似？如果相似，请给以证明；如果不相似，请说明理由．

Answer 1

【答案】（1）y=﹣x2+2x+3；（2）9（3）相似

【解析】

试题分析：（1）易得c=3，故设抛物线解析式为y=ax2+bx+3，根据抛物线所过的三点的坐标，可得方程组，解可得a、b的值，即可得解析式；

（2）易由顶点坐标公式得顶点坐标，根据图形间的关系可得四边形ABDE的面积=，代入数值可得答案；

（3）根据题意，易得∠AOB=∠DBE=90°，且，即可判断出两三角形相似．

试题解析：（1）∵抛物线与y轴交于点（0，3），

∴设抛物线解析式为y=ax2+bx+3（a≠0）

根据题意，得，

解得．

∴抛物线的解析式为y=﹣x2+2x+3；

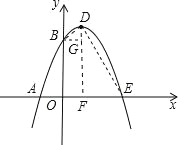
（2）如图，设该抛物线对称轴是DF，连接DE、BD．过点B作BG⊥DF于点G．

由顶点坐标公式得顶点坐标为D（1，4）

设对称轴与x轴的交点为F

∴四边形ABDE的面积=

=AOBO+（BO+DF）OF+EFDF

=×1×3+×（3+4）×1+×2×4

=9；

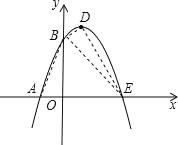
（3）相似，如图，

BD=；

∴BE=

DE==

∴BD2+BE2=20，DE2=20

即：BD2+BE2=DE2，

所以△BDE是直角三角形

∴∠AOB=∠DBE=90°，且，

∴△AOB∽△DBE．