【题目】如图,P是△ABC内一点,连结BP,并延长交AC于点D.
(1)试探究AB+BC+CA与2BD的大小关系;
(2)试探究AB+CA与PB+PC的大小关系.

参考答案:
【答案】(1)AB+BC+CA>2BD;(2)AB+CA>PB+PC.
【解析】
(1)根据三角形三边关系可得AB+AD>BD,BC+CD>BD,再根据不等式的性质即可求解;(2)根据三角形三边关系可得AB+AD>BD,PD+CD>PC,再根据不等式的性质即可求解.
解:(1)根据三角形三边关系可得AB+AD>BD,BC+CD>BD,
∴AB+AD+BC+CD>2BD,
∴AB+BC+CA>2BD.
(2)根据三角形三边关系可得AB+AD>BD,PD+CD>PC,
∴AB+AD+PD+CD>BD+PC,
∴AB+AD+CD>BD-PD+PC,
即AB+CA>PB+PC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,AD是△ABC的角平分线,△ABC的一个外角的平分线AE交边BC的延长线于点E,且∠BAD=20°,∠E=30°,则∠B的度数为________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某市正在进行商业街改造,商业街起点在古民居P的南偏西60°方向上的A处,现已改造至古民居P南偏西30°方向上的B处,A与B相距150m,且B在A的正东方向.为不破坏古民居的风貌,按照有关规定,在古民居周围100m以内不得修建现代化商业街.若工程队继续向正东方向修建200m商业街到C处,则对于从B到C的商业街改造是否违反有关规定?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ABC的两条角平分线相交于一点G,∠BAC=76°,∠ABE=20°,求∠BEC,∠ADC的度数.
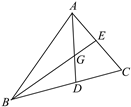
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F.
(1)当△PMN所放位置如图①所示时,求出∠PFD与∠AEM的数量关系;
(2)当△PMN所放位置如图②所示时,求证:∠PFD-∠AEM=90°;
(3)在(2)的条件下,若MN与CD交于点O,且∠DON=15°,∠PEB=30°,求∠N的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点O为直线AB上一点,过O点作射线OC,使∠AOC:∠BOC=1:2,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
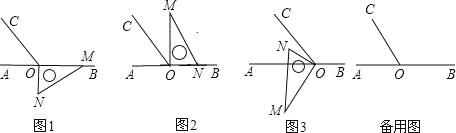
(1)将图1中的三角板绕点O按逆时针方向旋转至图2的位置,使得ON落在射线OB上,此时三角板旋转的角度为 度;
(2)继续将图2中的三角板绕点O按逆时针方向旋转至图3的位置,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由;
(3)在上述直角三角板从图1逆时针旋转到图3的位置的过程中,若三角板绕点O按15°每秒的速度旋转,当直角三角板的直角边ON所在直线恰好平分∠AOC时,求此时三角板绕点O的运动时间t的值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂有甲、乙两种型号的机器生产同样的产品,两种型号的机器一共48台,其中甲型号机器比乙型号机器多10台.
(1)乙型号机器有 台(请直接写出答案);
(2)若已知4台甲型号机器一天生产的产品装满6箱后还剩8个,5台乙型号机器的产品还缺1个就可以装满8箱,每台甲型号机器比每台乙型号机器一天多生产1个产品,求每箱装多少个产品?
(3)在前两问的条件下,若某天有2台甲型号机器和若干台乙型号机器同时开工,问这天生产的产品能否恰好装满35箱,请说明理由.
相关试题

