Question

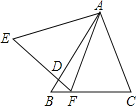
【题目】如图，△ABC与△AEF中，AB=AE，BC=EF，∠B=∠E，AB交EF于D．给出下列结论：

①∠AFC=∠C；

②DE=CF；

③△ADE∽△FDB；

④∠BFD=∠CAF

其中正确的结论是 ．

Answer 1

【答案】①③④

【解析】

试题分析：先根据已知条件证明△AEF≌△ABC，从中找出对应角或对应边．然后根据角之间的关系找相似，即可解答．

解：在△ABC与△AEF中

∵AB=AE，BC=EF，∠B=∠E

∴△AEF≌△ABC，

∴AF=AC，

∴∠AFC=∠C；

由∠B=∠E，∠ADE=∠FDB，

可知：△ADE∽△FDB；

∵∠EAF=∠BAC，

∴∠EAD=∠CAF，

由△ADE∽△FD，B可得∠EAD=∠BFD，

∴∠BFD=∠CAF．

综上可知：①③④正确．