【题目】下面是某同学对多项式(x2﹣4x+2)(x2﹣4x+6)+4进行因式分解的过程
解:设x2﹣4x=y,
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2﹣4x+4)2(第四步)
(1)该同学第二步到第三步运用了因式分解的 (填序号).
A.提取公因式 B.平方差公式
C.两数和的完全平方公式 D.两数差的完全平方公式
(2)该同学在第四步将y用所设中的x的代数式代换,得到因式分解的最后结果.这个结果是否分解到最后? .(填“是”或“否”)如果否,直接写出最后的结果 .
(3)请你模仿以上方法尝试对多项式(x2﹣2x)(x2﹣2x+2)+1进行因式分解.
参考答案:
【答案】(1)C;(2)否,(x﹣2)4;(3)(x2﹣2x)(x2﹣2x+2)+1=(x﹣1)4.
【解析】
(1)根据分解因式的过程直接得出答案;
(2)该同学因式分解的结果不彻底,进而再次分解因式得出即可;
(3)将![]() 看作整体进而分解因式即可.
看作整体进而分解因式即可.
(1)该同学第二步到第三步运用了因式分解的两数和的完全平方公式;
故选:C;
(2)这个结果没有分解到最后,
原式=(x2﹣4x+4)2=(x﹣2)4;
故答案为:否,(x﹣2)4;
(3)设为x2﹣2x=t,
则原式=t(t+2)+1
=t2+2t+1
=(t+1)2
=(x2﹣2x+1)2
=(x﹣1)4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是上海世博园内的一个矩形花园,花园长为100米,宽为50米,在它的四角各建有一个同样大小的正方形观光休息亭,四周建有与观光休息亭等宽的观光大道,其余部分(图中阴影部分)种植的是不同花草.已知种植花草部分的面积为3600米2,那么矩形花园各角处的正方形观光休息亭的边长为多少米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=3,连接DE.
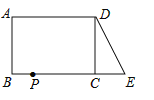
(1)DE的长为 .
(2)动点P从点B出发,以每秒1个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P运动的时间为t秒,求当t为何值时,△ABP和△DCE全等?
(3)若动点P从点B出发,以每秒1个单位的速度仅沿着BE向终点E运动,连接DP.设点P运动的时间为t秒,是否存在t,使△PDE为等腰三角形?若存在,请直接写出t的值;否则,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,BC=3,∠ABC和∠ACB的平分线相交于点O,OE∥AB,OF∥AC,则三角形OEF的周长为 .
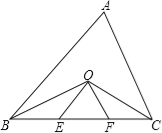
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC,按以下步骤作图:①分别以 B,C 为圆心,以大于
 BC 的长为半径作弧,两弧相交于两点 M,N;②作直线 MN 交 AB 于点 D,连接 CD.若 CD=AC,∠A=50°,则∠ACB 的度数为
BC 的长为半径作弧,两弧相交于两点 M,N;②作直线 MN 交 AB 于点 D,连接 CD.若 CD=AC,∠A=50°,则∠ACB 的度数为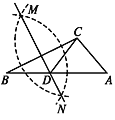
A.90°B.95°C.105°D.110°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
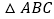 内接于
内接于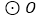 ,过点
,过点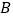 的切线与
的切线与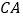 的延长线相交于点
的延长线相交于点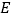 ,且
,且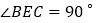 ,点
,点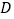 在
在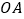 的延长线上,
的延长线上,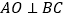 ,
,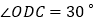 .
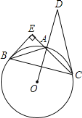
.
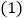 求证:
求证: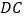 为
为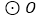 的切线.
的切线.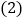 若
若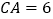 ,求
,求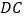 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】青海新闻网讯:2016年2月21日,西宁市首条绿道免费公共自行车租赁系统正式启用.市政府今年投资了112万元,建成40个公共自行车站点、配置720辆公共自行车.今后将逐年增加投资,用于建设新站点、配置公共自行车.预计2018年将投资340.5万元,新建120个公共自行车站点、配置2205辆公共自行车.
(1)请问每个站点的造价和公共自行车的单价分别是多少万元?
(2)请你求出2016年到2018年市政府配置公共自行车数量的年平均增长率.
相关试题

