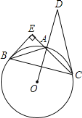
【题目】如图,![]() 内接于
内接于![]() ,过点
,过点![]() 的切线与
的切线与![]() 的延长线相交于点
的延长线相交于点![]() ,且
,且![]() ,点
,点![]() 在
在![]() 的延长线上,
的延长线上,![]() ,
,![]() .
.
![]() 求证:
求证:![]() 为
为![]() 的切线.
的切线.
![]() 若
若![]() ,求
,求![]() 的长.
的长.
参考答案:
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)连接![]() ,由半径
,由半径![]() 垂直于
垂直于![]() ,利用垂径定理得到
,利用垂径定理得到![]() 为
为![]() 的中点,可得出两条弧相等,根据等弧对等角可得出
的中点,可得出两条弧相等,根据等弧对等角可得出![]() ,又
,又![]() 为圆
为圆![]() 的切线,根据弦切角等于夹弧所对的圆周角可得出
的切线,根据弦切角等于夹弧所对的圆周角可得出![]() ,等量代换可得出三个角相等,由
,等量代换可得出三个角相等,由![]() 与
与![]() 垂直得到
垂直得到![]() 为直角,可得出三个角都为
为直角,可得出三个角都为![]() ,再利用同弧所对的圆心角等于所对圆周角的
,再利用同弧所对的圆心角等于所对圆周角的![]() 倍,可得出
倍,可得出![]() 为
为![]() ,又
,又![]() 为
为![]() ,在三角形
,在三角形![]() 中,利用三角形的内角和定理得到
中,利用三角形的内角和定理得到![]() 为
为![]() ,根据垂直的定义得到
,根据垂直的定义得到![]() 垂直于
垂直于![]() ,即可得出此时
,即可得出此时![]() 为圆
为圆![]() 的切线;
的切线;
(2)由![]() ,且
,且![]() 为
为![]() ,得到三角形
,得到三角形![]() 为等边三角形,根据等边三角形的三边长相等可得出
为等边三角形,根据等边三角形的三边长相等可得出![]() ,由
,由![]() 的长得出
的长得出![]() 的长,在直角三角形
的长,在直角三角形![]() 中,利用锐角三角函数定义表示出
中,利用锐角三角函数定义表示出![]() ,将
,将![]() 及
及![]() 的值代入即可求出
的值代入即可求出![]() 的长.
的长.
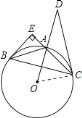
![]() 连接
连接![]() ,如图所示:
,如图所示:
∵![]() ,且
,且![]() 为圆心,
为圆心,
∴点![]() 为
为![]() 的中点,即
的中点,即![]() ,
,
∴![]() ,
,
又![]() 为切线,
为切线,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,又
,又![]() ,
,
∴![]() ,
,
∴![]() ,
,
则![]() 为圆
为圆![]() 切线;
切线;
![]() ∵
∵![]() ,
,![]() ,
,
∴![]() 为等边三角形,
为等边三角形,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
则![]() .
.
-
科目: 来源: 题型:
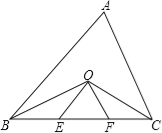
查看答案和解析>>【题目】已知如图,BC=3,∠ABC和∠ACB的平分线相交于点O,OE∥AB,OF∥AC,则三角形OEF的周长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是某同学对多项式(x2﹣4x+2)(x2﹣4x+6)+4进行因式分解的过程
解:设x2﹣4x=y,
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2﹣4x+4)2(第四步)
(1)该同学第二步到第三步运用了因式分解的 (填序号).
A.提取公因式 B.平方差公式
C.两数和的完全平方公式 D.两数差的完全平方公式
(2)该同学在第四步将y用所设中的x的代数式代换,得到因式分解的最后结果.这个结果是否分解到最后? .(填“是”或“否”)如果否,直接写出最后的结果 .
(3)请你模仿以上方法尝试对多项式(x2﹣2x)(x2﹣2x+2)+1进行因式分解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC,按以下步骤作图:①分别以 B,C 为圆心,以大于
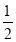 BC 的长为半径作弧,两弧相交于两点 M,N;②作直线 MN 交 AB 于点 D,连接 CD.若 CD=AC,∠A=50°,则∠ACB 的度数为
BC 的长为半径作弧,两弧相交于两点 M,N;②作直线 MN 交 AB 于点 D,连接 CD.若 CD=AC,∠A=50°,则∠ACB 的度数为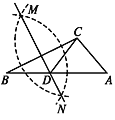
A.90°B.95°C.105°D.110°
-
科目: 来源: 题型:
查看答案和解析>>【题目】青海新闻网讯:2016年2月21日,西宁市首条绿道免费公共自行车租赁系统正式启用.市政府今年投资了112万元,建成40个公共自行车站点、配置720辆公共自行车.今后将逐年增加投资,用于建设新站点、配置公共自行车.预计2018年将投资340.5万元,新建120个公共自行车站点、配置2205辆公共自行车.
(1)请问每个站点的造价和公共自行车的单价分别是多少万元?
(2)请你求出2016年到2018年市政府配置公共自行车数量的年平均增长率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为( )秒时,△ABP和△DCE全等.

A. 1 B. 1或3 C. 1或7 D. 3或7
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程:x2﹣2(m+1)x+m2+5=0有两个不相等的实数根.
(1)求m的取值范围;
(2)若原方程的两个实数根为x1、x2, 且满足x12+x22=|x1|+|x2|+2x1x2,求m的值.
相关试题

