【题目】一个几何体由几个大小相同的小立方块搭成,从正面和上面观察这 个几何体,看到的形状都一样(如图所示).
(1)这个几何体最少有多少个小立方块,最多有多少个小立方块;
(2)当摆放的小立方块最多时,请画出从左面观察到的视图.

参考答案:
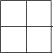
【答案】(1)该几何体最少有 7 个小正方体,最多有9 个小正方体,(2)由(1)知,该几何体的左视图如图所示:
【解析】
(1)易得这个几何体共有2层,由俯视图可得第一层立方体的个数,由主视图可得第二层立方体的可能的个数,相加即可.
(2)根据(1)中小正方体个数最多的情况的分布,由左视图的定义作图即可得.
(1)该几何体中小正方体的分布情况如图所示:
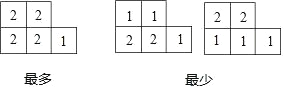
由图知,该几何体最少有 1+1+1+2+2=7 个小正方体,最多有 2+2+2+2+1=9 个小正方体,
(2)由(1)知,该几何体的左视图如图所示:
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一内部装有水的直圆柱形水桶,桶高20公分;另有一直圆柱形的实心铁柱,柱高30公分,直立放置于水桶底面上,水桶内的水面高度为12公分,且水桶与铁柱的底面半径比为2:1.今小贤将铁柱移至水桶外部,过程中水桶内的水量未改变,若不计水桶厚度,则水桶内的水面高度变为多少公分?( )

A.4.5
B.6
C.8
D.9 -
科目: 来源: 题型:
查看答案和解析>>【题目】表为小洁打算在某电信公司购买一支MAT手机与搭配一个门号的两种方案.此公司每个月收取通话费与月租费的方式如下:若通话费超过月租费,只收通话费;若通话费不超过月租费,只收月租费.若小洁每个月的通话费均为x元,x为400到600之间的整数,则在不考虑其他费用并使用两年的情况下,x至少为多少才会使得选择乙方案的总花费比甲方案便宜?( )
甲方案
乙方案
门号的月租费(元)
400
600
MAT手机价格(元)
15000
13000
注意事项:以上方案两年内不可变更月租费
A.500
B.516
C.517
D.600 -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:﹣3﹣(﹣5)+(﹣6)﹣(﹣3);
(2)计算:﹣23+(﹣4)×[(﹣1)2015+(﹣
 )2];
)2];(3)解方程:2x﹣(2﹣x)=4
(4)解方程:2﹣
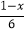 =
= ;
; -
科目: 来源: 题型:
查看答案和解析>>【题目】七中育才学校排球活动月即将开始,其中有一项为垫球比赛,体育组为了了解七年级学生的训练情况,随机抽取了七年级部分学生进行1分钟垫球测试,并将这些学生的测试成绩(即1分钟的个数,且这些测试成绩都在60~180范围内)分段后给出相应等级,具体为:测试成绩在60~90范围内的记为D级,90~120范围内的记为C级,120~150范围内的记为B级,150~180范围内的记为A级.现将数据整理绘制成如下两幅不完整的统计图,其中在扇形统计图中A级对应的圆心角为90°,请根据图中的信息解答下列问题:
(1)在扇形统计图中,A级所占百分比为 ;
(2)在这次测试中,一共抽取了 名学生,并补全频数分布直方图;
(3)在(2)中的基础上,在扇形统计图中,求D级对应的圆心角的度数;
(4)若A,B,C,D等级的平均成绩分别为165、135、105、75个,你能估算出学校七年级同学的平均水平吗?若能,请计算出来.(保留准确值)

-
科目: 来源: 题型:
查看答案和解析>>【题目】坐标平面上,某二次函数图形的顶点为(2,﹣1),此函数图形与x轴相交于P、Q两点,且PQ=6.若此函数图形通过(1,a)、(3,b)、(﹣1,c)、(﹣3,d)四点,则a、b、c、d之值何者为正?( )
A.a
B.b
C.c
D.d -
科目: 来源: 题型:
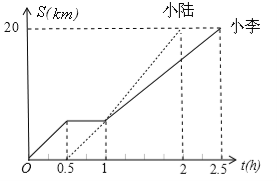
查看答案和解析>>【题目】小李和小陆从A地出发,骑自行车沿同一条路行驶到B地,他们离出发地的距离S(单位:km)和行驶时间t(单位:h)之间的函数关系的图象如图所示,根据图中的信息,有下列说法:
(1)他们都行驶了20 km;
(2)小陆全程共用了1.5h;
(3)小李和小陆相遇后,小李的速度小于小陆的速度
(4)小李在途中停留了0.5h。
其中正确的有
A.4个 B.3个 C.2个 D.1个
相关试题

