【题目】如图,在△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE,垂足为点E.连接DE, 则线段DE与线段AC有怎样的数量关系?请证明你的结论。
参考答案:
【答案】解:结论:AC=DE,理由如下:
∵CE⊥AE
∴∠AEC=90°
∵AE∥BC,
∴∠BCE=90°
∵AB=AC AD是BC边上的中线
∴∠ADC=90°
∴四边形ADCE是矩形
∴AC=D E
【解析】由CE⊥AE得∠AEC=90°;又AE∥BC, 根据两直线平行同旁内角互补得∠BCE=90°;再因为AB=AC AD是BC边上的中线;得出∠ADC=90°;从而得出四边形ADCE是矩形;根据矩形得性质得出AC=D E.
【考点精析】通过灵活运用平行线的性质,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰
 中,
中, ,
, , 底角为
, 底角为 ,动点
,动点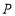 从点
从点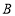 向点
向点 运动,当
运动,当 是直角三角形是
是直角三角形是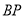 长为( )
长为( )A.4B.2或3C.3或4D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB∥CD,∠B=70°,∠BCE=20°,∠CEF=130°,请判断AB与EF的位置关系,并说明理由.
解: ,理由如下:
∵AB∥CD,
∴∠B=∠BCD,( )
∵∠B=70°,
∴∠BCD=70°,( )
∵∠BCE=20°,
∴∠ECD=50°,
∵∠CEF=130°,
∴ + =180°,
∴EF∥ ,( )
∴AB∥EF.( )

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边
 中取点
中取点 使得
使得 ,
, ,
, 的长分别为3, 4, 5,则
的长分别为3, 4, 5,则 _________.
_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1=80°,∠2=100°,∠C=∠D.
(1)判断AC与DF的位置关系,并说明理由;
(2)若∠C比∠A大20°,求∠F的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的文字,解答问题.
大家知道
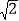 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此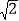 的小数部分我们不可能完全地写出来,于是小明用
的小数部分我们不可能完全地写出来,于是小明用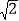 ﹣1来表示
﹣1来表示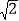 的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为
的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为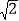 的整数部分是1,用这个数减去其整数部分,差就是小数部分.
的整数部分是1,用这个数减去其整数部分,差就是小数部分.请解答下列问题:
(1)求出
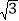 +2的整数部分和小数部分;
+2的整数部分和小数部分;(2)已知:10+
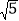 =x+y,其中x是整数,且0<y<1,请你求出(x﹣y)的相反数.
=x+y,其中x是整数,且0<y<1,请你求出(x﹣y)的相反数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形ABC中,AB=AC=2,∠B=75°,以C为旋转中心将△ABC顺时针旋转,当点B落在AB上点D处时,点A的对应点为E,则阴影部分面积为_____.

相关试题

