【题目】如图,在平面直角坐标系中,△ABC的顶点A、B分别落在x轴、y轴的正半轴上,顶点C在第一象限,BC与x轴平行.已知BC=2,△ABC的面积为1.
(1)求点C的坐标.
(2)将△ABC绕点C顺时针旋转90°,△ABC旋转到△A1B1C的位置,求经过点B1的反比例函数关系式.

参考答案:
【答案】(1)C(2,1);(2)经过点B1的反比例函数为y=![]() .
.
【解析】
(1)过点C作CD⊥x轴于点D,BC与x轴平行可知CD⊥BC,![]() 即可求出CD的长,进而得出C点坐标;
即可求出CD的长,进而得出C点坐标;
(2)由图形旋转的性质得出CB1的长,进而可得出B1的坐标,设经过点B1(2,3)的反比例函数为![]() ,把B1的坐标代入即可得出k的值,从而得出反比例函数的解析式.
,把B1的坐标代入即可得出k的值,从而得出反比例函数的解析式.
解:(1)作CD⊥x轴于D.
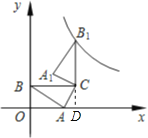
∵BC与x轴平行,
∴S△ABC=![]() BCCD,
BCCD,
∵BC=2,S△ABC=1,
∴CD=1,
∴C(2,1);
(2)∵由旋转的性质可知CB1=CB=2,
∴B1(2,3).
设经过点B1(2,3)的反比例函数为![]() ,
,
∴3=![]() ,
,
解得k=6,
∴经过点B1的反比例函数为y=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数分别填入相应的集合里
-4,
 ,
, 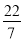 , 0, -3.14, 717, -(+5) +1.88,
, 0, -3.14, 717, -(+5) +1.88, 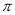
(1)正有理数集合:{_____________________________…}
(2)负数集合:{_____________________________…}
(3)整数集合:{_____________________________ …}
(4)分数集合:{______________________________…}
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一元二次方程中,有著名的韦达定理:对于一元二次方程ax2+bx+c=0(a≠0),如果方程有两个实数根x1,x2,那么x1+x2=﹣
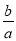 ,x1x2=
,x1x2=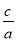 (说明:定理成立的条件△≥0).比如方程2x2﹣3x﹣1=0中,△=17,所以该方程有两个不等的实数解.记方程的两根为x1,x2,那么x1+x2=
(说明:定理成立的条件△≥0).比如方程2x2﹣3x﹣1=0中,△=17,所以该方程有两个不等的实数解.记方程的两根为x1,x2,那么x1+x2=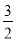 ,x1x2=﹣
,x1x2=﹣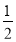 ,请根据阅读材料解答下列各题:
,请根据阅读材料解答下列各题:(1)已知方程x2﹣3x﹣2=0的两根为x1、x2,且x1>x2,求下列各式的值:
①x12+x22;②
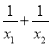 ;
;(2)已知x1,x2是一元二次方程4kx2﹣4kx+k+1=0的两个实数根.
①是否存在实数k,使(2x1﹣x2)(x1﹣2x2)=﹣
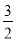 成立?若存在,求出k的值;若不存在,请说明理由.
成立?若存在,求出k的值;若不存在,请说明理由.②求使
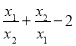 的值为整数的实数k的整数值.
的值为整数的实数k的整数值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,点E、F分别在AB、BC上,△DEF为等腰直角三角形,∠DEF=90°,AD+CD=10,AE=2,求AD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E为边AB上一点,连结DE,将ABCD沿DE翻折,使点A的对称点F落在CD上,连结EF.
(1)求证:四边形ADFE是菱形.
(2)若∠A=60°,AE=2BE=2.求四边形BCDE的周长.
小强做第(1)题的步骤
解:①由翻折得,AD=FD,AE=FE.
②∵AB∥CD.
③∴∠AED=∠FDE.
④∴∠AED=∠ADE
⑤∴AD=AE
⑥∴AD=AE=EF=FD
∴四边形ADFE是菱形.
(1)小强解答第(1)题的过程不完整,请将第(1)题的解答过程补充完整(说明在哪一步骤,补充什亻么条件或结论)
(2)完成题目中的第(2)小题.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级共有450名学生,随机抽取其中的若干名学生,根据这些学生两次数学模拟考试成绩,分别绘制了如下所示的频数分布直方图,其中图②不完整.

注:① 成绩均为整数;②“60以下”不含60,其余分数段均包含端点;③ 图①、图②分别表示第一次、第二次模拟考试成绩频数分布直方图.
根据以上信息,解答下列问题:
(1)把图②补全;
(2)规定100分以上为优秀,请计算图②中达到优秀的比例;
(3)请你估算九年级学生第二次数学模拟考试达到优秀的人数比第一次数学模拟考试增加多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某次世界魔方大赛吸引世界各地共900名魔方爱好者参加,本次大赛首轮进行3×3阶魔方赛,组委会随机将爱好者平均分到30个区域,每个区域30名同时进行比赛,完成时间小于8秒的爱好者进入下一轮角逐;如图是3×3阶魔方赛A区域30名爱好者完成时间统计图,
(1)填空:A区域3×3阶魔方爱好者进入下一轮角逐的有______人.
(2)填空:若A区域30名爱好者完成时间为9秒的人数是7秒人数的3倍,
①a=______,b=______;
②完成时间的平均数是______秒,中位数是______秒,众数是______秒.
(3)若3×3阶魔方赛各个区域的情况大体一致,则根据A区域的统计结果估计在3×3阶魔方赛后进入下一轮角逐的约有多少人?

相关试题

