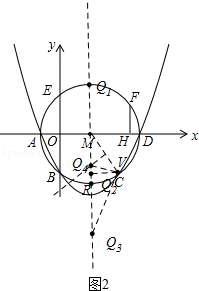
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c与⊙M相交于A、B、C、D四点,其中A、B两点的坐标分别为(﹣1,0),(0,﹣2),点D在x轴上且AD为⊙M的直径.点E是⊙M与y轴的另一个交点,过劣弧 ![]() 上的点F作FH⊥AD于点H,且FH=1.5
上的点F作FH⊥AD于点H,且FH=1.5
(1)求点D的坐标及该抛物线的表达式;
(2)若点P是x轴上的一个动点,试求出△PEF的周长最小时点P的坐标;
(3)在抛物线的对称轴上是否存在点Q,使△QCM是等腰三角形?如果存在,请直接写出点Q的坐标;如果不存在,请说明理由.
参考答案:
【答案】
(1)
解:连接BD,
∵AD是⊙M的直径,∴∠ABD=90°
∴△AOB∽△ABD,
∴ ![]() =
= ![]() ,
,
在Rt△AOB中,AO=1,BO=2,
根据勾股定理得:AB= ![]() ,
,
∴ ![]() ,
,
∴AD=5,
∴DO=AD﹣AO=5﹣1=4,
∴D(4,0),
把点A(﹣1,0)、B(0,﹣2)、D(4,0)代入y=ax2+bx+c可得:
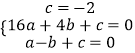 ,
,
解得: 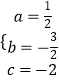 ,
,
∴抛物线表达式为: ![]()
(2)
解:连接FM,
在Rt△FHM中,FM= ![]() ,FH=
,FH= ![]() ,
,
∴MH= ![]() =2,
=2,
OM=AM﹣OA= ![]() ﹣1=
﹣1= ![]() ,
,
∴OH=OM+MH= ![]() +2=
+2= ![]() ,
,
∴F( ![]() ,
, ![]() ),
),
设直线BF的解析式为y=kx+b,
则: 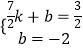 ,
,
∴直线BF的解析式为:y=x﹣2,
连接BF交x轴于点P,∵点E与点B关于x轴对称,
∴点P即为所求,
当y=0时,x=2,
∴P(2,0)
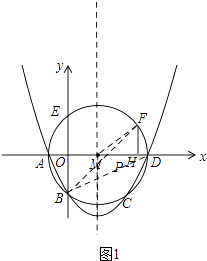
(3)
解:如图,CM= ![]()
抛物线 ![]() 的对称轴为直线x=
的对称轴为直线x= ![]() ,
,
∵OM= ![]() ,∴点M在直线x=
,∴点M在直线x= ![]() 上,
上,
根据圆的对称性可知,点C与点B关于直线x= ![]() 对称,
对称,
∴点C(3,﹣2),
①当CM=MQ= ![]() 时,点Q可能在x轴上方,也可能在x轴下方,
时,点Q可能在x轴上方,也可能在x轴下方,
∴Q1( ![]() ,
, ![]() ),Q2(
),Q2( ![]() ,
, ![]() ),
),
②当CM=CQ时,过点C作CN⊥MQ,
∴MN=NQ=2,∴MQ=4,
∴Q3( ![]() ,﹣4),
,﹣4),
③当CQ4=MQ4时,过点C作CR⊥MQ,Q4V⊥CM,
则:MV=CV= ![]() ,Q4V=
,Q4V= ![]() ,
,
Rt△CRM∽Rt△Q4VM,
∴ 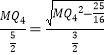 ,
,
解得:MQ4= ![]() ,
,
∴Q4( ![]() ,﹣
,﹣ ![]() )
)
综上可知,存在四个点,即:
Q1( ![]() ,
, ![]() ),Q2(
),Q2( ![]() ,
, ![]() ),Q3(
),Q3( ![]() ,﹣4),Q4(
,﹣4),Q4( ![]() ,﹣
,﹣ ![]() )
)
【解析】(1)首先根据圆的轴对称性求出点D的坐标,将A、B、D三点代入,即可求出本题的答案;(2)由于点E与点B 关于x轴对称,所以,连接BF,直线BF与x轴的交点,即为点P,据此即可得解;(3)从CM=MQ,CM=CQ,MQ=CQ三个方面进行分析,据此即可得解.
【考点精析】通过灵活运用二次函数的图象和二次函数的性质,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小即可以解答此题.
-
科目: 来源: 题型:
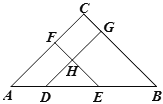
查看答案和解析>>【题目】如图,在△ABC中 ,∠A=∠B,D、E是边AB上的点,DG∥AC,EF∥BC,DG、EF相 交于点H.
(1)∠HDE与∠HED是否相等?并说明理由.
解:∠HDE=∠HED.理由如下:
∵DG∥AC(已知)
∴ = ( )
∵ EF∥BC (已知)
∴ = ( )
又∵∠A=∠B (已知)
∴ = ( ).
(2)如果∠C=90°,DG、 EF有何位置关系?并仿照 (1)中的解答方法说明理由.
解: .理由如下:
-
科目: 来源: 题型:
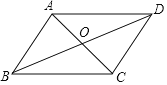
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AC与BD相交于点O,∠AOB=60°,BD=4,将△ABC沿直线AC翻折后,点B落在点E处,那么S△AED=______
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列解题过程的空白处填上适当的内容(推理的理由或数学表达式)
如图,已知AB∥CD,BE、CF分别平分∠ABC和∠DCB,求证:BE∥CF.
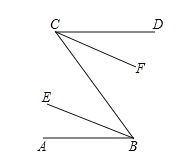
证明:∵AB∥CD,(已知)
∴∠_______=∠_______.___________________________
∵__________________________________________,(已知)
∴∠EBC=_______,(角平分线定义)
同理,∠FCB=______________.
∴∠EBC=∠FCB.(等式性质)
∴BE//CF.(_____________________________________)
-
科目: 来源: 题型:
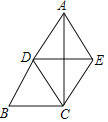
查看答案和解析>>【题目】已知:如图,在△ABC中,∠ACB=90°,点D是斜边AB的中点,DE∥BC,且CE=CD.
(1)求证:∠B=∠DEC;
(2)求证:四边形ADCE是菱形.
-
科目: 来源: 题型:
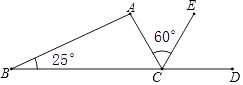
查看答案和解析>>【题目】如图,CE是△ABC的外角∠ACD的平分线,若∠B=25°,∠ACE=60°,则∠A=( )
A.105°
B.95°
C.85°
D.25° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=2x+4的图象与x,y轴分别相交于点A,B,以AB为边作正方形ABCD(点D落在第四象限).
(1)求点A,B,D的坐标;
(2)联结OC,设正方形的边CD与x相交于点E,点M在x轴上,如果△ADE与△COM全等,求点M的坐标.

相关试题

