Question

【题目】如图，在平面直角坐标系中，点A，B的坐标分别为A（0，α），B（b，α），且α、b满足（a﹣2）2+|b﹣4|=0，现同时将点A，B分别向下平移2个单位，再向左平移1个单位，分别得到点A，B的对应点C，D，连接AC，BD，AB．

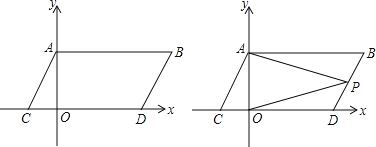
（1）求点C，D的坐标及四边形ABDC的面积S四边形ABCD

（2）在y轴上是否存在一点M，连接MC，MD，使S△MCD=S四边形ABDC？若存在这样一点，求出点M的坐标，若不存在，试说明理由．

（3）点P是线段BD上的一个动点，连接PA，PO，当点P在BD上移动时（不与B，D重合）的值是否发生变化，并说明理由．

Answer 1

【答案】（1）S四边形ABDC=8；（2）存在，M（0，4）或（0，﹣4）；（3）不变，理由见解析.

【解析】

试题分析：（1）先由非负数性质求出a=2，b=4，再根据平移规律，得出点C，D的坐标，然后根据四边形ABDC的面积=AB×OA即可求解；

（2）存在．设M坐标为（0，m），根据S△PAB=S四边形ABDC，列出方程求出m的值，即可确定M点坐标；

（3）过P点作PE∥AB交OC与E点，根据平行线的性质得∠BAP+∠DOP=∠APE+∠OPE=∠APO，故比值为1．

解：（1）∵（a﹣2）2+|b﹣4|=0，

∴a=2，b=4，

∴A（0，2），B（4，2）．

∵将点A，B分别向下平移2个单位，再向左平移1个单位，分别得到点A，B的对应点C，D，

∴C（﹣1，0），D（3，0）．

∴S四边形ABDC=AB×OA=4×2=8；

（2）在y轴上存在一点M，使S△MCD=S四边形ABCD．设M坐标为（0，m）．

∵S△MCD=S四边形ABDC，

∴×4|m|=8，

∴2|m|=8，

解得m=±4．

∴M（0，4）或（0，﹣4）；

（3）当点P在BD上移动时，=1不变，理由如下：

过点P作PE∥AB交OA于E．

∵CD由AB平移得到，则CD∥AB，

∴PE∥CD，

∴∠BAP=∠APE，∠DOP=∠OPE，

∴∠BAP+∠DOP=∠APE+∠OPE=∠APO，

∴=1．