【题目】已知数轴上两点A,B对应的数分别为﹣4,8.
(1)如图1,如果点P和点Q分别从点A,B同时出发,沿数轴负方向运动,点P的运动速度为每秒2个单位,点Q的运动速度为每秒6个单位.
①A,B两点之间的距离为 .
②当P,Q两点相遇时,点P在数轴上对应的数是 .
③求点P出发多少秒后,与点Q之间相距4个单位长度?
(3)如图2,如果点P从点A出发沿数轴的正方向以每秒2个单位的速度运动,点Q从点B出发沿数轴的负方向以每秒6个单位的速度运动,点M从数轴原点O出发沿数轴的正方向以每秒1个单位的速度运动,若三个点同时出发,经过多少秒后有MP=MQ?

参考答案:
【答案】(1)①12;②﹣10;③点P出发2或4秒后,与点Q之间相距4个单位长度;(2)三个点同时出发,经过![]() 或
或![]() 秒后有MP=MQ.
秒后有MP=MQ.
【解析】
(1)①根据两点间的距离公式即可求解;
②根据相遇时间=路程差÷速度差先求出时间,再根据路程=速度×时间求解即可;
③分两种情况:P,Q两点相遇前;P,Q两点相遇后;进行讨论即可求解;
(2)分两种情况:M在P,Q两点之间;P,Q两点相遇;进行讨论即可求解.
(1)①A,B两点之间的距离为8﹣(﹣4)=12,
故答案为:12;
②12÷(6﹣2)=3(秒),
﹣4﹣2×3=﹣10,
故当P,Q两点相遇时,点P在数轴上对应的数是﹣10,
故答案为:-10;
③P,Q两点相遇前,
(12﹣4)÷(6﹣2)=2(秒),
P,Q两点相遇后,
(12+4)÷(6﹣2)=4(秒),
故点P出发2或4秒后,与点Q之间相距4个单位长度;
(2)设三个点同时出发,经过t秒后有MP=MQ,
M在P,Q两点之间,
8﹣6t﹣t=t﹣(﹣4+2t),
解得t=![]() ;
;
P,Q两点相遇,
2t+6t=12,
解得t=![]() ,
,
故若三个点同时出发,经过![]() 或
或![]() 秒后有MP=MQ.
秒后有MP=MQ.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点 O 是直线 AB上一点,∠COD 是直角,OE平分∠BOC.
(1)①如图1,若∠DOE=25°,求∠AOC 的度数;
②如图2,若∠DOE=α,直接写出∠AOC的度数(用含α的式子表示);
(2)将图 1中的∠COD 绕点O按顺时针方向旋转至图 2 所示位置.探究∠DOE 与∠AOC 的度数之间的关系,写出你的结论,并说明理由.

-
科目: 来源: 题型:
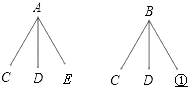
查看答案和解析>>【题目】某电脑店有A、B两种型号的打印机和C、D、E三种芯片出售.每种型号的打印机均需要一种芯片配套才能打印.
(1)下列是该店用树形图或列表设计的配套方案,①的位置应填写 , ②的位置应 填写
(2)若仅有B型打印机与E种芯片不配套,则上面(1)中的方案配套成功率是芯片
配套方案
打印机C
D
E
A
(A,C)
(A,D)
②
B
(B,C)
(B,D)
(B,E)
-
科目: 来源: 题型:
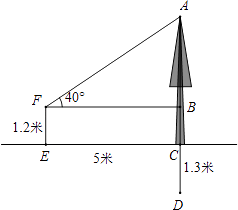
查看答案和解析>>【题目】如图,某校为搞好新校区的绿化,需要移植树木.该校九年级数学兴趣小组对某棵树木进行测量,此树木在移植时需要留出根部(即CD)1.3米.他们在距离树木5米的E点观测(即CE=5米),测量仪的高度EF=1.2米,测得树顶A的仰角∠BFA=40°,求此树的整体高度AD.(精确到0.1米)(参考数据:sin40°=0.6428,cos40°=0.7660,tan40°=0.8391)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文具店到批发市场选购A、B两种文具,批发价分别为14元/个、10元/个.若该店零售A、B两种文具的每天销量y(个)与零售价x(元/个)都是一次函数y=kx+20的关系,如图所示.
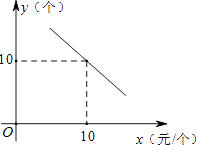
(1)求此一次函数的关系式;
(2)现批发市场进行促销活动,凭会员卡(240元/张)在该批发市场购买所有物品均进行打折优惠,若文具店购买A、B两种文具各50个,问打折小于多少折时,采用购买会员卡的方式合算;
(3)在文具店不购买会员卡的情况下,若A种文具零售价比B种文具零售价高2元/个,求这两种文具每天的销售总利润W(元)与A种文具零售价x(元/个)之间的函数关系式,并说明当A种文具的零售价为多少时,每天的销售利润最大. (说明:本题不要求写出自变量x的取值范围) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A、B、C、D、E在同一直线上,且AC=BD,E是线段BC的中点.
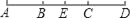
(1)点E是线段AD的中点吗?说明理由;
(2)当AD=10,AB=3时,求线段BE的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE是∠AOD的平分线,若∠AOC=60°,OF⊥OE.
(1)判断OF把∠AOC所分成的两个角的大小关系并证明你的结论;
(2)求∠BOE的度数.

相关试题

