【题目】如图,在菱形ABCD中,∠A=60°,E,F分别是AB,AD的中点,DE,BF相交于点G,连接BD,CG.有下列结论:
①∠BGD=120°;②BG+DG=CG;③△BDF≌△CGB;④S△ABD= ![]() AB2
AB2
其中正确的结论有( )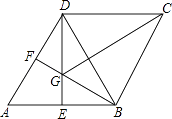
A.1个
B.2个
C.3个
D.4个
参考答案:
【答案】C
【解析】解:①由菱形的性质可得△ABD、BDC是等边三角形,∠DGB=∠GBE+∠GEB=30°+90°=120°,故①正确;
②∵∠DCG=∠BCG=30°,DE⊥AB,∴可得DG= ![]() CG(30°角所对直角边等于斜边一半)、BG=
CG(30°角所对直角边等于斜边一半)、BG= ![]() CG,故可得出BG+DG=CG,即②也正确;
CG,故可得出BG+DG=CG,即②也正确;
③首先可得对应边BG≠FD,因为BG=DG,DG>FD,故可得△BDF不全等△CGB,即③错误;
④S△ABD= ![]() ABDE=
ABDE= ![]() AB
AB ![]() BE=
BE= ![]() AB
AB ![]() AB=
AB= ![]() AB2 , 即④正确.
AB2 , 即④正确.
综上可得①②④正确,共3个.
故选C.
【考点精析】通过灵活运用菱形的性质,掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx-6经过点A(4,0),直线y=-3x+3与x轴交于点B,且两直线交于点C.
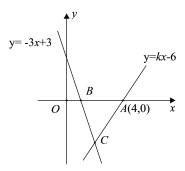
(1)求k的值;
(2)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“五一节”期间,王老师一家自驾游去了离家170千米的某地,下面是他们家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象,求当他们离目的地还有20千米时,汽车一共行驶的时间.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰△ABC中,AD⊥BC于点D,且AD=
 BC,则△ABC底角的度数为( )
BC,则△ABC底角的度数为( )
A.45°
B.75°
C.45°或15°或75°
D.60° -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,一次函数y=kx+b(k,b都是常数,且k≠0)的图象经过点(1,0)和(0,2).
(1)当﹣2<x≤3时,求y的取值范围;
(2)已知点P(m,n)在该函数的图象上,且m﹣n=4,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
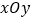 中,过点
中,过点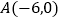 的直线
的直线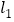 与直线
与直线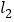 ;
;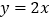 相交于点
相交于点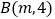 .
.(
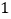 )求直线
)求直线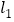 的表达式.
的表达式.(
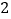 )过动点
)过动点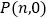 且垂于
且垂于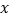 轴的直线与
轴的直线与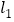 、
、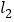 的交点分别为
的交点分别为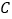 ,
,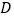 ,当点
,当点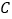 位于点
位于点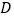 上方时,写出
上方时,写出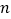 的取值范围.
的取值范围.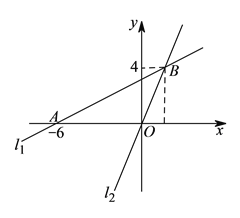
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长12的正方形ABCD中,有一个小正方形EFGH,其中E,F,G分别在AB,BC,FD上.若BF=3,则小正方形的边长为 .

相关试题

