【题目】结合数轴与绝对值的知识回答下列问题:

(1)数轴上表示4和1的两点之间的距离是________;表示![]() 和2两点之间的距离是______;一般地,数轴上表示数
和2两点之间的距离是______;一般地,数轴上表示数![]() 和数
和数![]() 的两点之间的距离等于
的两点之间的距离等于![]() .如果表示数
.如果表示数![]() 和
和![]() 的两点之间的距离是3,那么
的两点之间的距离是3,那么![]() _______.
_______.
(2)若数轴上表示数![]() 的点位于
的点位于![]() 与2之间,求
与2之间,求![]() 的值;
的值;
(3)受(2)的启发,当数![]() 的点在图1什么位置时,
的点在图1什么位置时,![]() 的值最小,最小值是多少?
的值最小,最小值是多少?
(4)有理数![]() 、
、![]() 、
、![]() 在数轴上对应的位置如图2所示,试化简:
在数轴上对应的位置如图2所示,试化简:![]() .
.
参考答案:
【答案】(1) 3 , 5 ,![]() 或1;(2)6;(3)7;(4)3a-c
或1;(2)6;(3)7;(4)3a-c
【解析】
(1)根据两点间的距离公式即可求解;
(2)先计算绝对值,再合并同类项即可求解;
(3)受(2)的启发,可知当数a的点位于5与2之间位置时,|a+5|+|a2|的值最小,进一步得到最小值;
(4)利用绝对值的意义化简,再合并同类项即可求解.
(1)数轴上表示4和1的两点之间的距离是41=3;表示3和2两点之间的距离是2(3)=5;
依题意有|a(2)|=3,
解得a=5或1.
故填:3 , 5 ,![]() 或1;
或1;
(2)∵数a的点位于4与2之间,
∴|a+4|+|a2|
=a+4a+2
=6;
(3)当数a的点在图1的5与2之间位置时,|a+5|+|a2|的值最小,最小值是2(5)=7;
(4)依题意有ba<0,bc<0,a+b>0,ab>0,
则|ba||bc|+|a+b|+|ab|=b+a+bc+a+b+ab=3ac.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列每对数在数轴上的对应点间的距离,3与5,4与﹣2, ﹣4与3, ﹣1与﹣5.并回答下列各题:

(1)数轴上表示4和﹣2两点间的距离是 ;表示﹣1和﹣5两点间的距离是 .
(2)若数轴上的点A表示的数为x,点B表示的数为﹣3.
①数轴上A、B两点间的距离可以表示为 (用含x的代数式表示);
②如果数轴上A、B两点间的距离为|AB|=1,求x的值.
(3)直接写出代数式
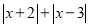 的最小值为 .
的最小值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】出租车司机小李某天上午营运时是在东西走向的大街上进行的,如果规定向东为正,向西为负,他这天上午所接六位乘客的行车里程(单位:
 )如下:
)如下: ,
, ,
, ,
, ,
, ,
, ,
,问:(1)将最后一位乘客送到目的地时,小李在什么位置?
(2)若汽车耗油量为
 (升/千米),这天上午小李接送乘客,出租车共耗油多少升?
(升/千米),这天上午小李接送乘客,出租车共耗油多少升?(3)若出租车起步价为8元,起步里程为
 (包括
(包括 ),超过部分每千米1.2元,问小李这天上午共得车费多少元?
),超过部分每千米1.2元,问小李这天上午共得车费多少元? -
科目: 来源: 题型:
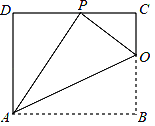
查看答案和解析>>【题目】如图,已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的点P处,折痕与BC交于点O.
(1)求证:△OCP∽△PDA;
(2)若PO:PA=1:2,则边AB的长是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,既是轴对称图形,又是中心对称图形的是( )
A.
 B.
B.  C.
C. 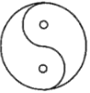 D.
D. 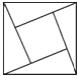
-
科目: 来源: 题型:
查看答案和解析>>【题目】工厂加工某种茶叶,计划一周生产
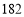 千克,平均每天生产
千克,平均每天生产 千克,由于各种原因实际每天产量与计划量相比有出入,某周七天的生产情况记录如下(超产为正、减产为负):
千克,由于各种原因实际每天产量与计划量相比有出入,某周七天的生产情况记录如下(超产为正、减产为负):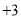 ,
, ,
,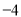 ,
,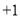 ,
,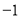 ,
,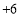 ,
,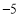 .
.(
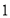 )这一周的实际产量是多少千克?
)这一周的实际产量是多少千克?(
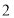 )该厂规定工人工资参照平均产量计发,每千克
)该厂规定工人工资参照平均产量计发,每千克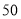 元.若超产,则超产的部分每千克
元.若超产,则超产的部分每千克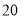 元;若低于平均产量,按实际产量计发,而且每少
元;若低于平均产量,按实际产量计发,而且每少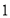 千克扣除
千克扣除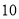 元,那么该工厂工人这一周的工资总额是多少?
元,那么该工厂工人这一周的工资总额是多少? -
科目: 来源: 题型:
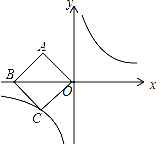
查看答案和解析>>【题目】如图,在平面直角坐标系中,正方形ABCO的对角线BO在x轴上,若正方形ABCO的边长为4
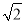 ,点B在x负半轴上,反比例函数的图象经过C点.
,点B在x负半轴上,反比例函数的图象经过C点.(1)求该反比例函数的解析式;
(2)若点P是反比例函数上的一点,且△PBO的面积恰好等于正方形ABCO的面积,求点P的坐标.
相关试题

