【题目】如图,在平面直角坐标系中,矩形![]() 的直角边
的直角边![]() 、
、![]() 分别在
分别在![]() 轴的正半轴和
轴的正半轴和![]() 轴的正半轴上,过点
轴的正半轴上,过点![]() 的直线
的直线![]() 交矩形的
交矩形的![]() 边于点
边于点![]() ,
, ![]() .
.
(1)求点![]() 的坐标(用含
的坐标(用含![]() 、
、![]() 的代数式表示);
的代数式表示);
(2)若把![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 恰好落在
恰好落在![]() 轴上的点
轴上的点![]() 处,
处,
①求![]() 与
与![]() 的函数关系式(不需写出
的函数关系式(不需写出![]() 的范围);
的范围);
②当![]() 时,在坐标轴上是否存在点
时,在坐标轴上是否存在点![]() ,使得
,使得![]() ,若存在,请求出点
,若存在,请求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.

参考答案:
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() 、
、![]() 、
、![]() 、
、![]()
【解析】试题分析:(1)由![]() ,可知点G纵坐标为b,把y=b代入
,可知点G纵坐标为b,把y=b代入![]() 中,解得
中,解得![]() ,可得点
,可得点![]() 的坐标.(2)① 由矩形性质可知
的坐标.(2)① 由矩形性质可知![]() 在
在![]() 中,令x=0,得y=b,得
中,令x=0,得y=b,得![]() ,由翻折
,由翻折![]() ,由一线三等角得
,由一线三等角得![]() ∽
∽![]() ,则对应边成比例,得
,则对应边成比例,得![]() ,在
,在![]() 中,由勾股定理可得
中,由勾股定理可得![]() 与
与![]() 的函数关系式;②
的函数关系式;②![]() ,可得
,可得![]() ,
, ![]() ,分情况讨论:
,分情况讨论: ![]() ,
, ![]() ,所以点
,所以点![]() 为符合题意的点;
为符合题意的点; ![]() 可得
可得![]() 轴,符合题意;在直线
轴,符合题意;在直线![]() 中,直线与
中,直线与![]() 轴的交点
轴的交点![]() ,也是符合题意的点;
,也是符合题意的点; ![]() 可知
可知![]() 是符合题意的点.
是符合题意的点.
试题解析:(1)当![]() 时,
时, ![]() ,解得:
,解得: ![]()
∴点![]() 的坐标为
的坐标为![]()
(2)①∵四边形![]() 是矩形,∴
是矩形,∴![]()
在![]() 中,当
中,当![]() 时,
时, ![]() ,
,
∴![]() ,又
,又![]() ,
,
∴![]() ,
,
∵![]() 与
与![]() 关于
关于![]() 对称,
对称,
∴![]() ,
, ![]() ,
,
∴![]()
又![]() ,
,
∴![]()
又![]() ,∴
,∴![]() ∽
∽![]() ,
,
∴![]() ,
, ![]() ,解得:
,解得: ![]() .
.
在![]() 中,由勾股定理得:
中,由勾股定理得: ![]() ,
, ![]() ,解得:
,解得: ![]() .
.
②![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
i) ![]() ,
, ![]() ,
,
∴点![]() 为符合题意的点,此时点
为符合题意的点,此时点![]() .
.
ii) ![]()

∴![]()
∵![]() ,∴
,∴![]() 轴,
轴, ![]() .
.
iii)在直线![]() 中,令
中,令![]() ,则
,则![]() ,
,
∴直线![]() 与
与![]() 轴的交点
轴的交点![]() ,
,
在![]() 中,
中, ![]() ,
,
∴点![]() 是符合题意的点.
是符合题意的点.
iv)点![]() 是关于
是关于![]() 的
的![]() 点为点
点为点![]() ,此时
,此时![]() ,
,
∴点![]() 是符合题意的点.
是符合题意的点.
综上,符合题意的点![]() 的坐标为
的坐标为![]() 、
、![]() 、
、![]() 、
、![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知同一平面内∠AOB=90°,∠AOC=60°.
(1)填空:∠BOC=__________;
(2)如果OD平分∠BOC,OE平分∠AOC,直接写出∠DOE的度数为_______;
(3)在(2)的条件下,将题目中∠AOC=60°改成∠AOC=
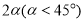 ,其它条件不变,请求出∠DOE的度数.
,其它条件不变,请求出∠DOE的度数.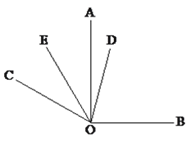
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校七年级共有学生600人,为了解这些学生的视力情况,抽查了50名学生的视力,并对所得数据进行了整理,在得到的频数分布表中,数据在0.95~1.15这一组频率为0.3,则可估计该校七年级学生视力在0.95~1.15范围内的人数为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列式子变形是因式分解的是( )
A. x2-2x-3=x(x-2)-3
B. x2-2x-3=(x-1)2-4
C. (x+1)(x-3)=x2-2x-3
D. x2-2x-3=(x+1)(x-3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l:y=x﹣
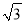 与x轴正半轴、y轴负半轴分别相交于A、C两点,抛物线y=
与x轴正半轴、y轴负半轴分别相交于A、C两点,抛物线y=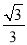 x2+bx+c经过点B(﹣1,0)和点C.
x2+bx+c经过点B(﹣1,0)和点C.(1)填空:直接写出抛物线的解析式:_____;
(2)已知点Q是抛物线y=
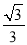 x2+bx+c在第四象限内的一个动点.
x2+bx+c在第四象限内的一个动点.①如图,连接AQ、CQ,设点Q的横坐标为t,△AQC的面积为S,求S与t的函数关系式,并求出S的最大值;
②连接BQ交AC于点D,连接BC,以BD为直径作⊙I,分别交BC、AB于点E、F,连接EF,求线段EF的最小值,并直接写出此时Q点的坐标.
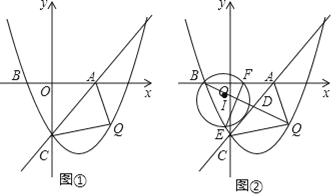
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年“五一”假期期间,某市接待旅游总人数达到了9 180 000人次,将9 180 000用科学记数法表示应为( )
A.918×104
B.9.18×105
C.9.18×106
D.9.18×107 -
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据1,2,3,3,5,4,10的中位数与众数分别是 ( )
A. 3,3 B. 5,3 C. 3,4 D. 5,10
相关试题

